
分析 由条件由sinB+cosB=$\sqrt{2}$得1+2sinBcosB=2,即sin2B=1,根据三角形的内角和定理得到0<B<180°得到B的度数.利用正弦定理求出A即可.
解答 解:由sinB+cosB=$\sqrt{2}$得1+2sinBcosB=2,即sin2B=1,
因为0<B<180°,所以B=45°,b=2,所以在△ABC中,
由正弦定理得:$\frac{\sqrt{2}}{sinA}=\frac{2}{sin45°}$,
解得sinA=$\frac{1}{2}$,又a<b,所以A<B=45°,所以A=30°.
故答案为:30°.
点评 本题考查了三角恒等变换、已知三角函数值求解以及正弦定理,考查了同学们解决三角形问题的能力,属于基础题.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
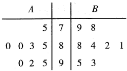 有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.
有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com