
分析 (1)先求出函数f(x)的导数,通过讨论a的范围,集合函数的单调性,从而求出函数的极值点;
(2)问题等价于g(x2)≤-f(x1),通过讨论b法范围,求出g(x)的最小值,从而求出b的最小值即可.
解答 解:(1)f′(x)=a-$\frac{1+a}{x}$+$\frac{1}{{x}^{2}}$=$\frac{a{x}^{2}-(a+1)x+1}{{x}^{2}}$=$\frac{(ax-1)(x-1)}{{x}^{2}}$,x>0-------(2分)
①若a>0,则
当$\frac{1}{a}$>1,即0<a<1时,f′(x)>0⇒0<x<1或x>$\frac{1}{a}$;f′(x)<0⇒1<x<$\frac{1}{a}$
f(x)的单调增区间为(0,1)和($\frac{1}{a}$,+∞),减区间为(1,$\frac{1}{a}$)
此时f(x)的极大值点为1,极小值点为$\frac{1}{a}$;
当$\frac{1}{a}$<1,即a>1时,同理,此时f(x)的极大值点为$\frac{1}{a}$,极小值点为1;
当a=1时,没有极值点;
②若a<0,则f′(x)>0⇒0<x<1;f′(x)<0⇒x>1
此时f(x)的极大值点为1,没有极小值点.
综上,若a<0,则f(x)的极大值点为1,没有极小值点;
若0<a<1,则f(x)的极大值点为1,极小值点为$\frac{1}{a}$;
若a=1,则没有极值点;
若a>1时,则f(x)的极大值点为$\frac{1}{a}$,极小值点为1.-------(6分)
(2)易知,f′(2)=0⇒a=$\frac{1}{2}$,由(1)可知函数f(x)的单调增区间为(0,1)和(2,+∞),减区间为(1,2),
又f(1)=-$\frac{1}{2}$,f(e)=$\frac{e}{2}$-$\frac{1}{e}$-$\frac{3}{2}$<-$\frac{1}{2}$,可知当x∈(0,e]时,≤-$\frac{1}{2}$
而f(x1)+g(x2)≤0?g(x2)≤-f(x1),又x1∈(0,e]时,
-f(x1)≥$\frac{1}{2}$由已知,应存在x∈[1,3],使得g(x)min≤$\frac{1}{2}$,-------(8分)
当b<0时,g(x)在[1,3]上递增,g(x)min=g(1)=1-b≤$\frac{1}{2}$⇒b≥$\frac{1}{2}$,不合题意;
当b>1时,g(x)在[1,3]上递减,g(x)min=g(3)=2-3b≤$\frac{1}{2}$⇒b≥$\frac{1}{2}$,故b>1,
当0≤b≤1时,若x∈[1,2],g(x)=1-bx,g(2)≤g(x)≤g(3),
若x∈[2,3],g(x)=(1-b)x-1,g(2)≤g(x)≤g(3),
故g(x)min=g(2)=1-2b≤$\frac{1}{2}$⇒b≥$\frac{1}{4}$,
故$\frac{1}{4}$≤b≤1,
综上,b≥$\frac{1}{4}$,即bmin=$\frac{1}{4}$.
点评 本题考查了函数的单调性、最值问题,考查分类讨论思想,导数的应用,熟练掌握导数的综合应用是解答此类问题的关键,本题难度较大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一个三棱锥的三视图,其俯视图是正三角形,主视图与左视图都是直角三角形.则这个三棱锥的外接球的表面积是( )
如图是一个三棱锥的三视图,其俯视图是正三角形,主视图与左视图都是直角三角形.则这个三棱锥的外接球的表面积是( )| A. | 19π | B. | 28π | C. | 67π | D. | 76π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
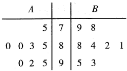 有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.
有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是梯形,DC∥AB,DC=2AB,O为AC与BD的交点,E是棱PA上一点,且OE∥平面PBC,求$\frac{AE}{PE}$的值.
如图,在四棱锥P-ABCD中,底面ABCD是梯形,DC∥AB,DC=2AB,O为AC与BD的交点,E是棱PA上一点,且OE∥平面PBC,求$\frac{AE}{PE}$的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com