
����Ŀ���������������ﻧ��������е������ݱ�����ϳ����˾ӻ����IJ��ϸ��ƣ����з��ز�סլ���ۼ۸�ڽ�������һ���ָ���ס�������˲�С�ķ��գ��±�Ϊ����2017.1��2017.5��5��סլ�۸����·ݵĹ�ϵ��
�·�x | 1 | 2 | 3 | 4 | 5 |
סլ�۸�y | 4.8 | 5.4 | 6.2 | 6.6 | 7 |
��1��ͨ�������������ϵ���ж�סլ��yǧԪ/ƽ�����·�x��������س̶ȣ���ȷ��0.01��
��2������С���˷��õ������Իع�ֱ��ȥ�������x��y�Ĺ�ϵ�� ����y����x�Ļع鷽�̣����Թ��ư������������ȥ�����ڲ��õ��ĸ����·ݣ����۽�ͻ����Ԫ/ƽ�Ĵ�أ�
���𰸡�
��1���⣺���ݱ������ݣ����� ![]() =
= ![]() ����1+2+3+4+5��=3��
����1+2+3+4+5��=3��
![]() =
= ![]() ����4.8+5.4+6.2+6.6+7��=6��
����4.8+5.4+6.2+6.6+7��=6��
����r=  =
= 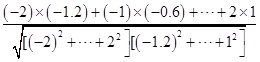 ��0.99��
��0.99��
���������ϵ��r�ж�סլ��yǧԪ/ƽ�����·�x��������س̶�ǿ
��2���⣺�ټ��� ![]() =
=  =
= ![]() ��0.56��
��0.56��
![]() =
= ![]() ��
�� ![]() =6��0.56��3=4.32��
=6��0.56��3=4.32��
��y����x�Ļع鷽��Ϊ ![]() =0.56x+4.32��
=0.56x+4.32��
���� ![]() =0.56x+4.32��10��
=0.56x+4.32��10��
���x��10.14��
Ӧȡ11�·ۣ����������������ȥ������2017���11�·ݣ����۽�ͻ����Ԫ/ƽ�Ĵ��
����������1�����ݱ������ݼ��� ![]() ��
�� ![]() ��������ϵ��r���ɣ���2���ټ���ع�ϵ����д���ع鷽�̣������ûع鷽�����
��������ϵ��r���ɣ���2���ټ���ع�ϵ����д���ع鷽�̣������ûع鷽����� ![]() ��10ʱx��ֵ�����ɵó����ۣ�
��10ʱx��ֵ�����ɵó����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2014��ɽ��ʡ�ڶ�ʮ�����˶��Ὣ�ڼ����ٿ���Ϊ��������ijУ�������Ƿ�Ը���ṩ־Ը�߷����ü�������������Ӹ�У������50�ˣ�������£�K
�Ƿ�Ը���ṩ־Ը�߷��� | Ը�� | ��Ը�� |
���� | 20 | 5 |
�� | 10 | 15 |
�����÷ֲ�����ķ�����Ը���ṩ־Ը�߷����ѧ���г�ȡ6�ˣ�����������ȡ�����ˣ�
�����ڣ����г�ȡ��6������ѡ2�ˣ���ǡ��һ��Ů���ĸ��ʣ�
�������ܷ���99%�İ�����Ϊ��У�������Ƿ�Ը���ṩ־Ը�߷������Ա��йأ�
������ٽ�ֵ�����ο���
P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�����Լ���ͳ���� ![]() ������n=a+b+c+d��
������n=a+b+c+d��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ��ԭ��OΪ���㣬x��������Ϊ���ᣬ������������ϵ��ȡ��ͬ�ij��ȵ�λ����ֱ֪��l�IJ�������Ϊ 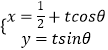 ����tΪ������0���ȣ��У�������C�ļ����귽��Ϊ��sin2����2cos��=0��
����tΪ������0���ȣ��У�������C�ļ����귽��Ϊ��sin2����2cos��=0��
��1��������C��ֱ�����귽�̣�
��2����ֱ��l������C�ཻ��A��B���㣬���ȱ仯ʱ����|AB|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ָ֪������![]() =
= ![]() ����
����![]() ������Ϊ
������Ϊ![]() �ĺ���
���![]() =
=![]() ���溯��.
���溯��.
(1)ȷ������![]() ��
��![]() �Ľ���ʽ;
�Ľ���ʽ;
(2)���������![]() ����ʽ
����ʽ![]() �����,��ʵ��
�����,��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ħ������ߵ�������108�ף�ֱ������98�ף�������תһȦ��Ҫ18���ӣ����ij�˴�Ħ���ֵ���͵�![]() ������Ħ���ֲ���ʼ��ʱ����ô��
������Ħ���ֲ���ʼ��ʱ����ô��
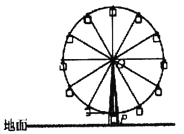
��1�������˵��Ĵξ������![]() ��ʱ���˶��ٷ��ӣ�
��ʱ���˶��ٷ��ӣ�
��2�������˾�����治����![]() ��ʱ���Կ���������ȫò����Ħ������תһȦ���ж��ٷ��ӿ��Կ���������ȫò��
��ʱ���Կ���������ȫò����Ħ������תһȦ���ж��ٷ��ӿ��Կ���������ȫò��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ݺ���![]() Ϊż����.
Ϊż����.
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��������![]() ������
������![]() ��Ϊ������������ʵ��
��Ϊ������������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=xlnx�� ![]() x2��x+a��a��R
x2��x+a��a��R
��1����a=0ʱ������f��x���ļ�ֵ��
��2��������f��x�����䶨��������������ͬ�ļ�ֵ�㣨��ֵ����ָ����ȡ��ֵʱ��Ӧ���Ա�����ֵ������Ϊx1 �� x2 �� ��x1��x2 �� ��������a��ȡֵ��Χ��
������������ʽe1+����x1x ![]() �����������ʵ���˵�ȡֵ��Χ��
�����������ʵ���˵�ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��ֱ��
��ֱ�� ![]() ��������
�������� ![]() ��
�� ![]() ��û�н��㣻��֪����
��û�н��㣻��֪���� ![]() ������
������ ![]() ��ʾ˫���ߣ���
��ʾ˫���ߣ��� ![]() Ϊ�棬
Ϊ�棬 ![]() Ϊ�٣�����ʵ��
Ϊ�٣�����ʵ�� ![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��
��1���жϺ���![]() ����ż�ԣ�������֤����
����ż�ԣ�������֤����
��2����![]() ʱ��ʹ
ʱ��ʹ![]() ��
��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com