练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知．

    （1）判断函数的奇偶性，并予以证明；

    （2）当时求使的的取值范围．

    【答案】（1）函数f（x）是奇函数（2）（0，1）

    【解析】试题分析：(1)先求出函数的定义域为（-1，1）,对任意,求出,由此得到函数是奇函数.

    (2)由, ,得,由此利用对数函数性质能求出不等式的解集.

    试题解析：（1）由，可得-1＜x＜1，∴函数f（x）的定义域为（-1，1）关于原点对称； f（-x）=loga（1-x）-loga（1+x）=-f（x），

    ∴函数f（x）是奇函数；

    （2）f（x）＞0，即loga（1+x）-loga（1-x）＞0，

    即， a＞1，等价于，等价于1+x＞1-x，又等价于x＞0．

    故对a＞1，当x∈（0，1）时有f（x）＞0．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】近来景德镇市棚户区改造进行的如火如荼，加上城市人居环境的不断改善，我市房地产住宅销售价格节节攀升，一部分刚需住户带来了不小的烦恼，下表为我市2017.1﹣2017.5这5月住宅价格与月份的关系．

    月份x

    1

    2

    3

    4

    5

    住宅价格y
    千元/平米

    4.8

    5.4

    6.2

    6.6

    7


    （1）通过计算线性相关系数判断住宅价y千元/平米与月份x的线性相关程度（精确到0.01）
    （2）用最小二乘法得到的线性回归直线去近似拟合x，y的关系． ①求y关于x的回归方程；②试估计按照这个趋势下去，将在不久的哪个年月份，房价将突破万元/平米的大关．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图（甲），在直角梯形中， ， ， ，且， ， 、、分别为、、的中点，现将沿折起，使平面平面，如图（乙）．

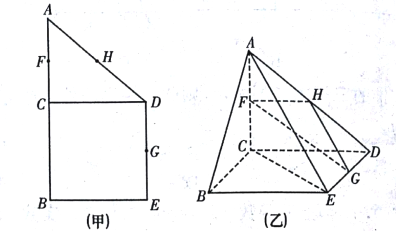
    （1）求证：平面平面；

    （2）若，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线l1过点A(0,1)，l2过点B(5,0)，如果l1∥l2，且l1与l2的距离为5，求l1、l2的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数y=loga（x+3）﹣1（a＞0且a≠1）的图象恒过定点A，若点A在mx+ny+2=0上，其中mn＞0，则 的最小值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥中，底面是边长为1的正方形，侧棱底面，且， 是侧棱上的动点.

    （1）求四棱锥的表面积；

    （2）是否在棱上存在一点，使得平面；若存在，指出点的位置，并证明；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某港口水的深度是时间，单位： 的函数，记作.下面是某日水深的数据：

    经长期观察， 的曲线可以近似地看成函数的图象.一般情况下，船舶航行时，船底离海底的距离为或以上时认为是安全的（船舶停靠时，船底只需不碰海底即可）.

    （1）求与满足的函数关系式；

    （2）某船吃水程度（船底离水面的距离）为，如果该船希望在同一天内安全进出港，请问它同一天内最多能在港内停留多少小时？（忽略进出港所需的时间）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知复数z=（m2+5m﹣6）+（m2﹣2m﹣15）i，（i为虚数单位，m∈R）
    （1）若复数Z在复平面内对应的点位于第一、三象限的角平分线上，求实数M的值；
    （2）当实数m=﹣1时，求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为调查大学生这个微信用户群体中每人拥有微信群的数量，现从武汉市大学生中随机抽取100位同学进行了抽样调查，结果如下：

    微信群数量

    频数

    频率

    0至5个

    0

    0

    6至10个

    30

    0.3

    11至15个

    30

    0.3

    16至20个

    a

    c

    20个以上

    5

    b

    合计

    100

    1

    （Ⅰ）求a，b，c的值；
    （Ⅱ）以这100个人的样本数据估计武汉市的总体数据且以频率估计概率，若从全市大学生（数量很大）中随机抽取3人，记X表示抽到的是微信群个数超过15个的人数，求X的分布列和数学期望．

    查看答案和解析>>

    同步练习册答案