练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f（x）=|x-1|+|x-a|．如果?x∈R，f（x）≥2，求a的取值范围为
     
    ．
    考点：绝对值不等式的解法
    专题：不等式的解法及应用
    分析：依题意，只需f（x）min≥2，利用绝对值不等式易求得f（x）min=|a-1|，故只需解不等式|a-1|≥2即可．
    解答： 解：∵?x∈R，f（x）=|x-1|+|x-a|≥2，
    ∴f（x）min≥2，
    ∵f（x）=|x-1|+|a-x|≥|x-1+a-x|=|a-1|，
    ∴|a-1|≥2，
    ∴a-1≤-2，a-1≥2
    解得：a≤-1，a≥3，
    ∴a的取值范围为（-∞，-1]∪[3，+∞）．
    故答案为：（-∞，-1]∪[3，+∞）．
    点评：本题考查绝对值不等式的解法，理解题意，求得f（x）min=|a-1|是关键，考查等价转化思想与运算求解能力，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

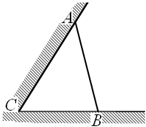    如图所示，某建筑工地准备建造一间两面靠墙的三角形露天仓库堆放材料，已知已有两面墙CA、CB的夹角为60°（即∠ACB=60°），现有可供建造第三面围墙的材料6米（两面墙的长均大于6米），为了使得仓库的面积尽可能大，记∠ABC=θ，问当θ为多少时，所建造的三角形露天仓库的面积最大，并求出最大值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知抛物线C：y2=2px（p＞0），点A、B在抛物线C上．
    （Ⅰ）若直线AB过点M（2p，0），且|AB|=4p，求过A，B，O（O为坐标原点）三点的圆的方程；
    （Ⅱ） 设直线OA、OB的倾斜角分别为α，β且α+β=
    π
    4
    ，问直线AB是否会过某一定点？若是，求出这一定点的坐标，若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    2sin20°+cos10°+tan20°sin10°=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，CD=1，BC=2，P为线段AD（含端点）上一个动点．设
    AP
    =x
    AD
    ，
    PB
    •
    PC
    =y，记y=f（x），则f（1）=
     
    ； 函数f（x）的值域为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，已知tanA=
    3
    4
    ，
    CA
    •
    AB
    =-8，则BC边的最小值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数y=f（x）为偶函数，当x≥0时，f（x）=（
    1
    2
    ）x，则不等式f（x）≥
    1
    2
    的解集为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在Rt△ABC中，∠B=90°，AB=1，BC=
    		3
    ，在边AB，AC上分别取D、E两点，使沿线段DE折叠三角形时，顶点A正好落在边BC上的点A′处，在这种情况下，则A′E最小值=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）=x2+ax，x∈R，常数a∈R，则（　　）
    A、存在a，使f（x）是奇函数
    B、存在a，使f（x）是偶函数
    C、?a∈R，f（x）在（0，+∞）上是增函数
    D、?a∈R，f（x）在（-∞，0）上是减函数

    查看答案和解析>>

    同步练习册答案