练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．袋中装有大小相同的4个红球和6个白球，从中取出4个球．
    （1）若取出的球必须是两种颜色，则有多少种不同的取法？
    （2）若取出的红球个数不少于白球个数，则有多少种不同的取法？

    分析 （1）用间接法分析：先计算从袋子中取出4个球的取法数目，再计算并排除其中颜色相同的取法数目，即可得答案；
    （2）分3种情况讨论：①、4个全部是红球，②、有3个红球，1个白球，③、有2个红球，2个白球，分别求出每种情况下的取法数目，由分类计数原理计算可得答案．

    解答 解：（1）根据题意，袋中装有大小相同的4个红球和6个白球，从中取出4个，有C104=210种取法，
    其中颜色相同的情况有2种：4个红球或4个白球，
    若4个红球，有C44=1种取法，
    若4个白球，有C64=15种取法，
    则取出球必须是两种颜色的取法有210-（1+15）=194种；
    （2）若取出的红球个数不少于白球个数，分3种情况讨论：
    ①、4个全部是红球，有C44=1种取法，
    ②、有3个红球，1个白球，有C43C61=24种取法，
    ③、有2个红球，2个白球，有C42C62=90种取法，
    则一共有1+24+90=115种取法．

    点评 本题考查排列、组合的综合应用，注意球与球之间只有颜色不同．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．与-30°终边相同的角是（　　）
    A．-330°B．150°C．30°D．330°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若cos α＞0，sin α＜0，则角 α的终边在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．用数列归纳法证明$\frac{1}{2}+cosα+cos2α+…+cosnα=\frac{{sin（n+\frac{1}{2}）α}}{{2sin\frac{α}{2}}}$时，验证n=1时，左边式子为（　　）
    A．$\frac{1}{2}$B．cosαC．$\frac{1}{2}+cosα$D．$\frac{{sin\frac{3}{2}α}}{{2sin\frac{α}{2}}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+$…$+\frac{1}{n（n+1）}$=$\frac{n}{n+1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

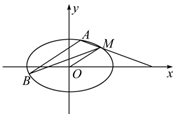    17．如图，已知椭圆C的中心在原点，它的一个焦点与抛物线${y^2}=4\sqrt{6}x$的焦点相同，又椭圆C上有一点M（2，1），直线l平行于OM且与椭圆C交于A，B两点，连接MA，MB．
    （1）求椭圆C的方程；
    （2）求证：直线MA，MB与x轴所构成的三角形总是以x轴上所在线段为底边的等腰三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知函数$f（x）=2sin（ωx+ϕ）（ω＞0，0＜ϕ＜\frac{π}{2}）$，$f（-\frac{π}{4}）=0$，$f（\frac{π}{4}-x）=f（\frac{π}{4}+x）$，且f（x）在$（\frac{π}{18}，\frac{2π}{9}）$上单调，则ω的最大值为5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．如图所示的三棱柱ABC-A1B1C1中，底面是正三角形，侧棱BB1⊥面ABC，D是棱BC的中点，点M在棱BB1上，且CM⊥AC1．
    （1）求证：A1B∥平面AC1D；
    （2）求证：CM⊥C1D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某工厂为了对新研发的一种产品进行合理定价，将该定价按事先拟定的价格进行试销，得到如下数据：
    单价x（元）88.28.48.68.89
    销量y（元）908483807568
    （1）求回归直线方程$\hat y=bx+a$；
    （2）预计在今后的销售中，销量与单价仍然服从（1）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？
    附：$b=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）}（{{y_i}-\overline y}）}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}，a=\overline y-b\overline x$．

    查看答案和解析>>

    同步练习册答案