
分析 根据f(-$\frac{π}{4}$)=0和$f(\frac{π}{4}-x)=f(\frac{π}{4}+x)$,求出φ=$\frac{π}{4}$,ω=-4k+1,k∈Z;
根据f(x)在$(\frac{π}{18},\frac{2π}{9})$上单调,得出$\frac{2π}{9}$-$\frac{π}{18}$≤$\frac{T}{2}$,从而求出ω的最大值.
解答 解:函数f(x)=2sin(ωx+φ),
∴f(-$\frac{π}{4}$)=2sin(-$\frac{π}{4}$ω+φ)=0,
∴-$\frac{π}{4}$ω+φ=kπ,k∈Z①;
又$f(\frac{π}{4}-x)=f(\frac{π}{4}+x)$,
∴x=$\frac{π}{4}$是f(x)图象的对称轴,
∴$\frac{π}{4}$ω+φ=k′π+$\frac{π}{2}$,k′∈Z②;
由①②得,φ=$\frac{k+k′}{2}$π+$\frac{π}{4}$,k∈Z,
∴取φ=$\frac{π}{4}$,且ω=-4k+1,k∈Z;
∴f(x)=2sin(ωx+$\frac{π}{4}$)的最小正周期为T=$\frac{2π}{ω}$;
又f(x)在$(\frac{π}{18},\frac{2π}{9})$上单调,
∴$\frac{2π}{9}$-$\frac{π}{18}$≤$\frac{π}{ω}$,即$\frac{1}{6}$≤$\frac{1}{ω}$,
解得ω≤6;
综上,ω的最大值为5.
故答案为:5.
点评 本题考查了正弦型函数的图象与性质的应用问题,是中档题.


科目:高中数学 来源: 题型:选择题
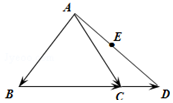 在△ABC中,已知D是BC延长线上一点,点E为线段AD的中点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,且$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则λ=( )
在△ABC中,已知D是BC延长线上一点,点E为线段AD的中点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,且$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则λ=( )| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 4 | 7 | a1,3 | … | a1,j |
| 7 | 12 | a2,3 | … | a2,j |
| a | a3,2 | a3,3 | … | a3,j |
| … | … | … | … | … |
| ai,1 | ai,2 | ai,3 | … | ai,j |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}π$ | B. | $\frac{1}{3}π$ | C. | $\frac{5}{6}π$ | D. | $\frac{2}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com