
已知函数f(x)=logkx(k为常数,k>0且k≠1),且数列{f(an)}是首项为4,公差为2的等差数列。
(1)求证:数列{an}是等比数列;
(2)若bn=an·f(an),当k=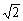 时,求数列{bn}的前n项和Sn。
时,求数列{bn}的前n项和Sn。
(1)证明:由题意知f(an)=4+(n-1)×2=2n+2, …………(2分)
即logkan=2n+2,∴an=k2n+2, …………(3分)
∴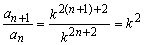 . …………(5分)
. …………(5分)
∵常数k>0且k≠1,∴k2为非零常数,
∴数列{an}是以k4为首项,k2为公比的等比数列。 …………(6分)
(2)由(1)知,bn=anf(an)=k2n+2·(2n+2),
当k=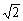 时,bn=(2n+2)·2n+1=(n+1)·2n+2. …………(8分)
时,bn=(2n+2)·2n+1=(n+1)·2n+2. …………(8分)
∴Sn=2·23+3·24+4·25+…+(n+1)·2n+2, ①
2Sn=2·24+3·25+…+n·2n+2+(n+1)·2 n+3, ② …………(10分)
②-①,得Sn=―2·23―24―25―…―2n+2+(n+1)·2n+3
=―23―(23+24+25+…+2n+2)+(n+1)·2n+3,
∴Sn=―23―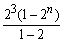 +(n+1)·2n+3=n·2n+3. …………(12分)
+(n+1)·2n+3=n·2n+3. …………(12分)


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
已知函数f(x)=ax3+ x2在x=-1处取得极大值,记g(x)=
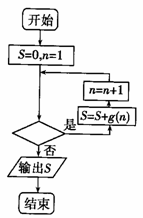
x2在x=-1处取得极大值,记g(x)=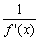 。程序框图如图所示,若输出的结果
。程序框图如图所示,若输出的结果
S=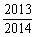 ,则判断框中可以填入的关于n的判断条件是
,则判断框中可以填入的关于n的判断条件是
A.n≤2013 B.n≤2014 C.n>2013 D.n>2014
查看答案和解析>>
科目:高中数学 来源: 题型:
设点P是双曲线 与圆x2+y2=a2+b2的一个交点,F1, F2分别是双曲线的左、右焦点,且|
与圆x2+y2=a2+b2的一个交点,F1, F2分别是双曲线的左、右焦点,且|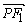 |=
|=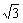 |
|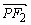 |,则双曲线的离心率为
|,则双曲线的离心率为
A.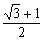 B.
B.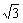 +1 C.
+1 C.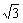 D.2
D.2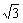
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com