
| A. | (-∞,-e) | B. | (-∞,-e] | C. | (-e,0) | D. | [-e,0) |
分析 求出l关于y轴的对称直线方程,把直线l上有且只有两个点关于y轴的对称点在曲线Γ:y=ex上,转化为直线y=-kx与y=ex有两个交点,然后求出过原点与曲线Γ:y=ex相切的直线的斜率得答案.
解答 解:直线l:y=kx关于y轴的对称直线方程为y=-kx,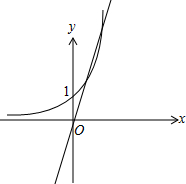
要使直线l上有且只有两个点关于y轴的对称点在曲线Γ:y=ex上,
则直线y=-kx与y=ex有两个交点,
如图,设过原点的直线切曲线y=ex于P(${x}_{0},{e}^{{x}_{0}}$),
由y=ex,得y′=ex,∴$y′{|}_{x={x}_{0}}={e}^{{x}_{0}}$,
则切线方程为y-${e}^{{x}_{0}}$=${e}^{{x}_{0}}$(x-x0),
把O(0,0)代入,可得x0=1,
∴切线的斜率k=e1=e,
∴-k>e,则k<-e.
∴k的取值范围是(-∞,-e).
故选:A.
点评 本题考查利用导数研究过曲线上某点处的切线方程,考查数学转化思想方法,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
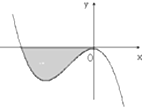 已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点相切,且x轴与函数图象所围成的区域(如图阴影部分)的面积为$\frac{1}{12}$,则a的值为-1.
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点相切,且x轴与函数图象所围成的区域(如图阴影部分)的面积为$\frac{1}{12}$,则a的值为-1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. | 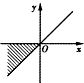 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com