
(本题满分14分)
已知函数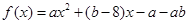 ,当
,当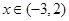 时,
时,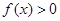 ;
;
当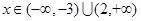 时,
时,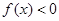 .
.
(1)求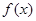 在
在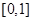 内的值域;
内的值域;
(2)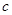 为何值时,
为何值时,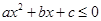 的解集为
的解集为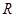 .
.
(1)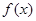 在
在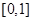 内的值域为
内的值域为 .
.
(2)当 时,
时,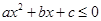 的解集为
的解集为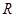 .
.
解析试题分析:由题意可得当x=-3和x=2时,有y=0,代入可求a,b,进而可求f(x)
(1)由二次函数的性质可判断其在[0,1]上的单调性,进而可求函数的值域
(2)令g(x)=-3x2+5x+c,要使g(x)≤0的解集为R.则△≤0,解不等式可求
解:由题意可知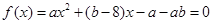 的两根分别为
的两根分别为 ,且
,且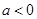 ,则由韦达定理可得:
,则由韦达定理可得: .
.
故 ,
,
(1)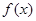 在
在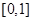 内单调递减,故
内单调递减,故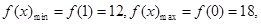
故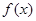 在
在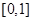 内的值域为
内的值域为 .
.
(2) ,则要使
,则要使 的解集为R,只需要方程
的解集为R,只需要方程 的判别式
的判别式 ,即
,即 ,解得
,解得 .
.
∴当 时,
时,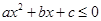 的解集为
的解集为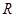 .
.
考点:本试题主要考查了二次函数、二次方程及二次不等式之间的关系的相互转化,二次函数性质的应用及二次不等式的求解,属于知识的简单应用。
点评:解决该试题的关键是对于二次函数单调性性质的运用,以及二次不等式的恒陈立问题的等价转化。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com