
若偶函数f(x)在区间(-∞,-1]上是增函数,则 ( )
A.f(- )<f(-1)<f(2)
)<f(-1)<f(2)
B.f(-1)<f(- )<f(2)
)<f(2)
C.f(2)<f(-1)<f(- )
)
D.f(2)<f(- )<f(-1)
)<f(-1)
科目:高中数学 来源:2016届河南省原名校高三上学期第一次联考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数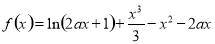 (
( ).
).
(1)若 为
为 的极值点,求实数
的极值点,求实数 的值;
的值;
(2)若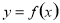 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(3)当 时,函数
时,函数 有零点,求实数
有零点,求实数 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁省大连市高二10月月考数学试卷(解析版) 题型:选择题
右图是用模拟方法估计圆周率 的程序框图,
的程序框图, 表示估计结 果,则图中空白框内应填入( )
表示估计结 果,则图中空白框内应填入( )

A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年广东省英德市高二上学期第一次月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)某厂拟用集装箱托运甲、乙两种货物,集装箱的体积、重量、可获利润和托运能力等限制数据列在下表中,如何设计甲、乙两种货物应各托运的箱数可以获得最大利润,最大利润是多少?.
货物 | 体积(m3/箱) | 重量(50 kg/箱) | 利润(百元/箱) |
甲 | 5 | 2 | 20 |
乙 | 4 | 5 | 10 |
托运限制 | 24 | 13 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年广东省普宁市高一上学期期中考试数学试卷(解析版) 题型:解答题
(本小题满分14分)
(1)已知△ABC三个顶点的坐标分别为A(4,1),B(0,3),C(2,4),边AC的中点为D,求AC边上中线BD所在的直线方程并化为一般式;
(2)已知圆C的圆心是直线 和
和 的交点且与直线
的交点且与直线 相切,求圆C的方程.
相切,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年甘肃省定西市高一上学期第一次月考数学试卷(解析版) 题型:选择题
集合{0,2, 3}的真子集共有( )
A、5个 B、6个 C、7个 D、8个
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市高一下学期期末考试数学试卷(解析版) 题型:解答题
(本题满分8分) 本题共有2个小题,第1小题4分,第2小题4分.
已知 ,
, ,且函数
,且函数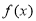 图象上的任意两条对称轴之间距离的最小值是
图象上的任意两条对称轴之间距离的最小值是 .
.
(1)求 的值;
的值;
(2)将函数 的图像向右平移
的图像向右平移 个单位后,得到函数
个单位后,得到函数 的图像,求函数
的图像,求函数 的解析式,并求
的解析式,并求 在
在 上的最值.
上的最值.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川成都市六校高一上学期期中联考数学试卷(解析版) 题型:选择题
对于函数 的定义域中任意的
的定义域中任意的 、
、
 ,有如下结论:
,有如下结论:
① ;
;
② ;
;
③ ;
;
④ .
.
当 时,上述结论中正确的有( )个
时,上述结论中正确的有( )个
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年福建厦门双十中学高二上期中理科数学试卷(解析版) 题型:解答题
(本小题满分14分)
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/时的航行速度匀速行驶,经过t小时与轮船相遇.

(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(Ⅱ)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com