分析:(1)先证明BC⊥AC,由AA
1⊥平面ABC,可得AA
1⊥BC,利用线面垂直的判定,可得结论;
(2)分别取BB
1中点M和AB中点E,可得平面EMD∥平面AB
1C
1,从而DE∥平面AB
1C
1;
(3)建立空间直角坐标系,求出平面ABB
1的一个法向量
=(
,0,1),
=(0,-,-)是平面AB
1C
1的一个法向量,且
<,>与二面角B-AB
1-C
1的大小相等,从而可求二面角B-AB
1-C
1的余弦值的大小.
解答:(1)证明:在矩形ACC
1A
1中,AA
1=
,AC1=3,AB=2,BC=1
∴AB
2=AC
2+BC
2∴BC⊥AC
∵AA
1⊥平面ABC,
∴AA
1⊥BC
∵AA
1∩AC=A
∴BC⊥平面ACC
1A
1;
(2)解:分别取BB
1中点M和AB中点E,由DM∥B
1C
1,EM∥AB
1,得平面EMD∥平面AB
1C
1,∴DE∥平面AB
1C
1,
即E为AB中点时,DE∥平面AB
1C
1;
(3)解:以C为坐标原点,CB,CC
1,CA所在直线分别为x轴、y轴、z轴建立空间直角坐标系,

则C(0,0,0),B(1,0,0),A(0,0,
),C
1(0,
,0),B
1(1,
,0),A
1(0,
,
),D(0,
,0)
设
=(x,y,z)是平面ABB
1的一个法向量
由
可得
,∴可取
=(
,0,1)
∵
=(0,-,-)是平面AB
1C
1的一个法向量,且
<,>与二面角B-AB
1-C
1的大小相等
∴cos
<,>=
=-
∴所求二面角B-AB
1-C
1的余弦值的大小为-
.
点评:本题主要考查二面角的计算,直线和平面垂直、平行的性质、判定,考查学生空间想象能力,计算能力、转化能力

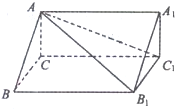 (2012•黄冈模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=
(2012•黄冈模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AA1=


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案