【题目】已知椭圆
离心率为
，点
与椭圆的左、右顶点可以构成等腰直角三角形．点C是椭圆的下顶点，经过椭圆中心O的一条直线与椭圆交于A，B两个点（不与点C重合），直线CA，CB分别与x轴交于点D，E．
（1）求椭圆的标准方程．
（2）判断
的大小是否为定值，并证明你的结论．
走进文言文系列答案科目：高中数学 来源： 题型：
【题目】某工厂在两个车间
，
内选取了12个产品，它们的某项指标分布数据的茎叶图如图所示，该项指标不超过19的为合格产品.
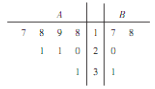
（1）从选取的产品中在两个车间分别随机抽取2个产品，求两车间都至少抽到一个合格产品的概率；
（2）若从车间，选取的产品中随机抽取2个产品，用
表示车间内产品的个数，求的分布列与数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，∠ABD=∠CBD，AB=BD．
（1）证明：平面ACD⊥平面ABC；
（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，求二面角D–AE–C的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设有编号为1，2，3，4，5的五把锁和对应的五把钥匙．现给这5把钥匙也贴上编号为1，2，3，4，5的五个标签，则共有______种不同的贴标签的方法：若想使这5把钥匙中至少有2把能打开贴有相同标签的锁，则有______种不同的贴标签的方法．（本题两个空均用数字作答）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】每年9月第三个公休日是全国科普日．某校为迎接2019年全国科普日，组织了科普知识竞答活动，要求每位参赛选手从4道“生态环保题”和2道“智慧生活题”中任选3道作答（每道题被选中的概率相等），设随机变量ξ表示某选手所选3道题中“智慧生活题”的个数．
（Ⅰ）求该选手恰好选中一道“智慧生活题”的概率；
（Ⅱ）求随机变量ξ的分布列及数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝x3
ax2﹣x+1（a∈R）．
（1）当a＝2时，求曲线y＝f（x）在点（1，f （1））处的切线方程；
（2）当a＜0时，设g（x）＝f（x）+x．
①求函数g（x）的极值；
②若函数g（x）在[1，2]上的最小值是﹣9，求实数a的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在如图所示的几何体中，四边形
是正方形，
平面，
，
分别是线段
，
的中点，
．
（I）在棱
上找一点
，使得平面
平面
，请写出点的位置，并加以证明；
（Ⅱ）求点到平面的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市图书馆准备进一定量的书籍，由于不同年龄段对图书的种类需求不同，为了合理配备资源，现对该市看书人员随机抽取了一天60名读书者进行调查.将他们的年龄分成6段：
，
后得到如图所示的频率分布直方图，问：
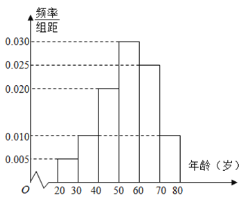
（1）在60名读书者中年龄分布在
的人数；
（2）估计60名读书者年龄的平均数和中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
