
已知 的三个顶点
的三个顶点 ,
,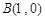 ,
,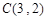 ,其外接圆为
,其外接圆为 .
.
(1)若直线 过点
过点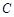 ,且被
,且被 截得的弦长为2,求直线
截得的弦长为2,求直线 的方程;
的方程;
(2)对于线段 上的任意一点
上的任意一点 ,若在以
,若在以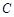 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点 ,使得点
,使得点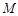 是线段
是线段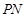 的中点,求
的中点,求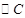 的半径
的半径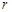 的取值范围.
的取值范围.
(1) 或
或 ;(2)
;(2)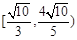 .
.
解析试题分析:(1)求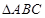 的外接圆方程可用待定系数法或利用两边垂直平分线的交点先求出圆心,再利用两点之间距离公式求出半径,求出圆的方程后再利用待定系数法求出直线的方程,此时要注意分直线斜率存在和不存在两种情况讨论;(2)可设出点
的外接圆方程可用待定系数法或利用两边垂直平分线的交点先求出圆心,再利用两点之间距离公式求出半径,求出圆的方程后再利用待定系数法求出直线的方程,此时要注意分直线斜率存在和不存在两种情况讨论;(2)可设出点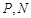 的坐标,再把点
的坐标,再把点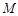 的坐标用其表示,把点
的坐标用其表示,把点 的坐标代入圆的方程,利用方程组恒有解去考察半径的取值范围,但要注意
的坐标代入圆的方程,利用方程组恒有解去考察半径的取值范围,但要注意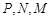 三点不能重合,即圆和线段
三点不能重合,即圆和线段 无公共点.
无公共点.
试题解析:(1)线段 的垂直平分线方程为
的垂直平分线方程为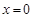 ,线段
,线段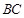 的垂直平分线方程为
的垂直平分线方程为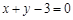 ,所以外接圆圆心
,所以外接圆圆心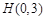 ,半径
,半径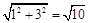 ,
, 的方程为
的方程为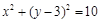 . 4分
. 4分
设圆心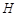 到直线
到直线 的距离为
的距离为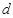 ,因为直线
,因为直线 被
被 截得的弦长为2,所以
截得的弦长为2,所以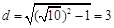 .
.
当直线 垂直于
垂直于 轴时,显然符合题意,即
轴时,显然符合题意,即 为所求; 6分
为所求; 6分
当直线 不垂直于
不垂直于 轴时,设直线方程为
轴时,设直线方程为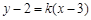 ,则
,则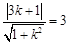 ,解得
,解得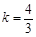 ,
,
综上,直线 的方程为
的方程为 或
或 . 8分
. 8分
(2) 直线 的方程为
的方程为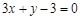 ,设
,设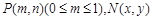 ,
,
因为点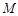 是点
是点 ,
,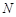 的中点,所以
的中点,所以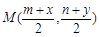 ,又
,又 都在半径为
都在半径为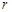 的
的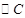 上,
上,
所以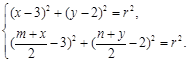 即
即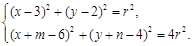 10分
10分
因为该关于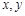 的方程组有解,即以
的方程组有解,即以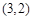 为圆心
为圆心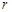 为半径的圆与以
为半径的圆与以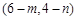 为圆心
为圆心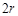 为半径的圆有公共点,所以
为半径的圆有公共点,所以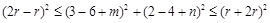 , 12分
, 12分
又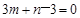 ,所以
,所以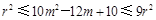 对
对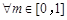 ]成立.
]成立.
而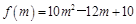 在[0,1]上的值域为[,10],故
在[0,1]上的值域为[,10],故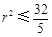 且
且 . 15分
. 15分
又线段 与圆
与圆 无公共点,所以
无公共点,所以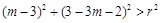 对
对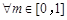 成立,即
成立,即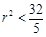 .故
.故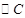 的半径
的半径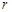 的取值范围为
的取值范围为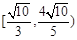 . 16分
. 16分
考点:圆的方程,直线与圆的位置关系,圆与圆的位置关系.


科目:高中数学 来源: 题型:解答题
已知圆 ,设点B,C是直线
,设点B,C是直线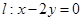 上的两点,它们的横坐标分别是
上的两点,它们的横坐标分别是 ,点P在线段BC上,过P点作圆M的切线PA,切点为A
,点P在线段BC上,过P点作圆M的切线PA,切点为A
(1)若 ,求直线
,求直线 的方程;
的方程;
(2)经过 三点的圆的圆心是
三点的圆的圆心是 ,求线段
,求线段 (
(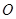 为坐标原点)长的最小值
为坐标原点)长的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知圆心为C的圆,满足下列条件:圆心C位于x轴正半轴上,与直线3x-4y+7=0相切,且被 轴截得的弦长为
轴截得的弦长为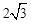 ,圆C的面积小于13.
,圆C的面积小于13.
(Ⅰ)求圆C的标准方程;
(Ⅱ)设过点M(0,3)的直线l与圆C交于不同的两点A,B,以OA,OB为邻边作平行四边形OADB.是否存在这样的直线l,使得直线OD与MC恰好平行?如果存在,求出l的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知圆 过点
过点 ,且圆心
,且圆心 在直线
在直线 上。
上。
(I)求圆 的方程;
的方程;
(II)问是否存在满足以下两个条件的直线 : ①斜率为
: ①斜率为 ;②直线被圆
;②直线被圆 截得的弦为
截得的弦为 ,以
,以 为直径的圆
为直径的圆 过原点. 若存在这样的直线,请求出其方程;若不存在,说明理由.
过原点. 若存在这样的直线,请求出其方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知点 和圆
和圆 :
: .
.
(Ⅰ)过点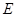 的直线
的直线 被圆
被圆 所截得的弦长为
所截得的弦长为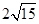 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)若 的面积
的面积 ,且
,且 是圆
是圆 内部第一、二象限的整点(平面内横、纵坐标均为整数
内部第一、二象限的整点(平面内横、纵坐标均为整数
的点称为整点),求出点 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知圆 和点
和点 (1)若过点
(1)若过点 有且只有一条直线与圆
有且只有一条直线与圆 相切,求正实数
相切,求正实数 的值,并求出切线方程;(2)若
的值,并求出切线方程;(2)若 ,过点
,过点 的圆的两条弦
的圆的两条弦 互相垂直,设
互相垂直,设 分别为圆心到弦
分别为圆心到弦 的距离.
的距离.
(Ⅰ)求 的值;
的值;
(Ⅱ)求两弦长之积 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com