
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
【答案】(1)an=2n-1,n∈N*;(2)n的最小值为10.
【解析】试题分析:本题属于基础题.对已知条件![]() ,用
,用![]() 代替
代替![]() 得
得![]() ,两式相减可得
,两式相减可得![]() ,凑配得
,凑配得![]() ,由此可证得
,由此可证得![]() 是等比数列,从而求出通项公式,这是已知数列前
是等比数列,从而求出通项公式,这是已知数列前![]() 项和与项之间关系的一般处理方法;(2)由(1)可得
项和与项之间关系的一般处理方法;(2)由(1)可得![]() ,采用错位相减法可求出其前
,采用错位相减法可求出其前![]() 项和
项和![]()
![]() ,不等式>2 010就转化为
,不等式>2 010就转化为![]() ,可知n的最小值是10.
,可知n的最小值是10.
试题解析:(1)因为Sn+n=2an,所以Sn-1=2an-1-(n-1)(n≥2,n∈N*).两式相减,得an=2an-1+1.
所以an+1=2(an-1+1)(n≥2,n∈N*),所以数列{an+1}为等比数列.
因为Sn+n=2an,令n=1得a1=1.
a1+1=2,所以an+1=2n,所以an=2n-1.
(2)因为bn=(2n+1)an+2n+1,所以bn=(2n+1)·2n.
所以Tn=3×2+5×22+7×23+…+(2n-1)·2n-1+(2n+1)·2n, ①
2Tn=3×22+5×23+…+(2n-1)·2n+(2n+1)·2n+1, ②
①-②,得-Tn=3×2+2(22+23+…+2n)-(2n+1)·2n+1
=6+2×-(2n+1)·2n+1
=-2+2n+2-(2n+1)·2n+1=-2-(2n-1)·2n+1.
所以Tn=2+(2n-1)·2n+1.
若>2 010,
则>2 010,即2n+1>2 010.
由于210=1 024,211=2 048,所以n+1≥11,即n≥10.
所以满足不等式>2 010的n的最小值是10.


科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是![]() .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: 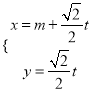 (
(![]() 是参数).
是参数).
(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,将直线![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)若直线l与曲线C相交于A、B两点,且![]() ,试求实数m的值.
,试求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣2x﹣8≤0},B={x| ![]() <0},U=R.
<0},U=R.
(1)求A∪B;
(2)求(UA)∩B;
(3)如果C={x|x﹣a>0},且A∩C≠,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(I)求函数![]() 的对称轴方程;
的对称轴方程;
(II)将函数![]() 的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移
的图象上各点的纵坐标保持不变,横坐标伸长为原来的2倍,然后再向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.若
的图象.若![]() 分别是△ABC三个内角A,B,C的对边,a=2,c=4,且
分别是△ABC三个内角A,B,C的对边,a=2,c=4,且![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的解析式满足 ![]() .
.
(1)求函数f(x)的解析式;
(2)当a=1时,试判断函数f(x)在区间(0,+∞)上的单调性,并加以证明;
(3)当a=1时,记函数 ![]() ,求函数g(x)在区间
,求函数g(x)在区间 ![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求曲线![]() 的直角坐标方程,并指出其表示何种曲线;
的直角坐标方程,并指出其表示何种曲线;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,
,
试求当![]() 时,
时, ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 上一点,平面
上一点,平面![]() 与棱
与棱![]() 交于点
交于点![]() .
.

(Ⅰ)求证: ![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)若![]() ,试问平面
,试问平面![]() 是否可能与平面
是否可能与平面![]() 垂直?若能,求出
垂直?若能,求出![]() 值;若不能,说明理由。
值;若不能,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com