已知数列{an}的前n项和是Sn,且2Sn=2-an.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ) 记bn=an+n,求数列{bn}的前n项和Tn.
解:(Ⅰ)当n=1时,2S
1=2-a
1,2a
1=2-a
1,∴
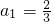
;
当n≥2时,
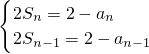
,
两式相减得2a
n=a
n-1-a
n(n≥2),
即3a
n=a
n-1(n≥2),又a
n-1≠0∴

(n≥2),
∴数列a
n是以

为首项,

为公比的等比数列,
∴
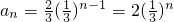
.
(Ⅱ)由(Ⅰ)知,
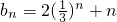
,
∴
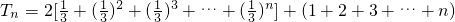
=

=
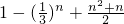
.
分析:(Ⅰ)根据a
n=s
n-s
n-1(n≥2)和题意进行求解,再由等比数列的通项公式求出;
(Ⅱ)由(Ⅰ)的结果求出b
n,根据b
n的特点需要用拆项法求该数列的前n项和,还利用等比数列前n项和公式进行求解.
点评:本小题主要考查等比数列及数列求和等基础知识,以及数列的前n项和与通项公式的关系式,利用拆项法求数列的前n项和,考查运算求解能力.

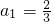 ;
;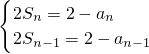 ,
, (n≥2),
(n≥2), 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,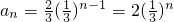 .
.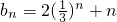 ,
,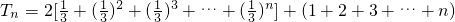 =
=
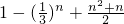 .
.
