
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
将函数f(x)=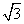 sin2x+cos2x(xR)的图象向左平移
sin2x+cos2x(xR)的图象向左平移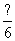 个单位长度后得到函数y=g(x)的图象,则函数y=g(x) ( )
个单位长度后得到函数y=g(x)的图象,则函数y=g(x) ( )
A.是奇函数 B.是偶函数
C.既是奇函数又是偶函数 D.既不是奇函数,也不是偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
定义[x]表示不超过x的最大整数,记{x}=x-[x],其中对于0≤x≤316时,函数f(x)=sin2[x]+sin2{x}-1和函数g(x)=[x]·{x}- -1的零点个数分别为m,n则 ( )
-1的零点个数分别为m,n则 ( )
A.m=101,n=314 B.m=101,n=313 C.m=100,n=313 D.m=100,n=314
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)是在(0,+∞)上处处可导的函数,若xf ′(x)>f(x)在x>0上恒成立:
(1)判断函数g(x)=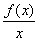 在(0,+∞)上的单调性;
在(0,+∞)上的单调性;
(2)当x1>0,x2>0时,证明f(x1)+f(x2)<f(x1+x2);
(3)求证: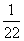 ln22+
ln22+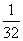 ln32+
ln32+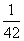 ln42+…
ln42+… 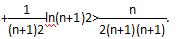
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数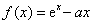 (e为自然对数的底数).
(e为自然对数的底数).
(Ⅰ)讨论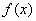 的单调性;
的单调性;
(Ⅱ)定义:函数 的定义域为
的定义域为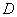 ,若
,若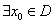 ,使
,使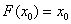 成立,则称
成立,则称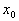 为
为 的不动点.
的不动点.
当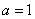 时,
时,
(ⅰ)证明:函数 存在唯一的不动点
存在唯一的不动点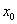 ,且
,且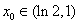 ;
;
(ⅱ)已知数列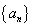 满足
满足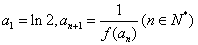 ,
,
求证: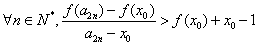 ,(其中
,(其中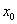 为
为 的不动点).
的不动点).
查看答案和解析>>
科目:高中数学 来源: 题型:
二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)在区间[-1,1]上,函数y=f(x)的图像恒在直线y=2x+m的上方,试确定实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com