
分析 首先看出至少有两个人的生日是同一个月的对立事件,对立事件是7个人中没有人的生日在同一个月,这是一个等可能事件的概率,试验发生包含的事件数127,满足条件的事件是7个人生日分别在7个月,共有A127种结果,根据古典概型概率公式得到结果.
解答 解:设至少有两个人的生日是同一个月为事件A,
则$\overline{A}$表示7个人中没有人的生日在同一个月,
P($\overline{A}$)=$\frac{{A}_{12}^{7}}{1{2}^{7}}$,
∴根据对立事件的概率得到:
P(A)=1-P($\overline{A}$)=1-$\frac{{A}_{12}^{7}}{1{2}^{7}}$.
点评 本题是一个生日问题,考查对立事件的概率,对立事件是指同一次试验中,不会同时发生的事件,遇到求用至少来表述的事件的概率时,往往先求它的对立事件的概率.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)在区间$[{\frac{π}{8},\frac{5π}{8}}]$上是减函数 | |
| B. | 直线x=$\frac{π}{8}$是函数f(x)图象的一条对称轴 | |
| C. | 若$x∈[{0,\frac{π}{2}}]$,则函数f(x)的值域是$[{0,\sqrt{2}}]$ | |
| D. | 函数f(x)的图象可由函数y=$\sqrt{2}$sin2x的图象向左平移$\frac{π}{8}$而得到 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
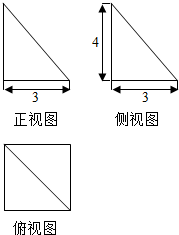
| A. | $\frac{1}{4}π$ | B. | 3π | C. | 4π | D. | $\frac{4}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}•\overrightarrow{b}$=0 | B. | $\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | C. | $\overrightarrow{a}•\overrightarrow{b}$=-|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com