【答案】
分析:(1)先设x∈[-e,0)则-x∈(0,e],再求出f(-x)利用函数是奇函数求出f(x),最后用分段函数表示出函数的解析式;
(2)由(1)知x∈[-e,0)时f(x)的解析式,再构造函数
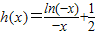
,分别求出这两个函数的导函数和符号,判断出它们在区间[-e,0)的单调性,并求出f(x)的最小值和h(x)的最大值,判断出最小值比最大值大,则不等式成立;
(3)先假设存在实数a满足条件,再求出x∈[-e,0)时f(x)的导函数
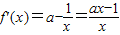
,对a的符号分类讨论来确定f'(x)的符号,进而判断出在区间[-e,0)上的单调性,求出最小值和m的值,注意验证范围是否符合.
解答:解:(1)设x∈[-e,0),则-x∈(0,e],∴f(-x)=-ax+ln(-x),
又∵f(x)是定义在[-e,0)∪(0,e]上的奇函数,
∴f(x)=-f(-x)=ax-ln(-x),
∴函数f(x)的解析式为
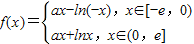
(2)证明:当x∈[-e,0)且a=-1时,
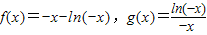
,
设
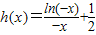
,
∵
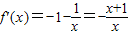
,
∴当-e≤x≤-1时,f'(x)≤0,此时f(x)单调递减;
当-1<x<0时,f'(x)>0,此时f(x)单调递增,
∴f(x)
min=f(-1)=1>0,
又∵
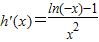
,
∴当-e≤x<0时,h'(x)≤0,此时h(x)单调递减,
∴
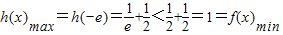
∴当x∈[-e,0)时,f(x)>h(x),即
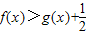
(3)解:假设存在实数a,使得当x∈[-e,0)时,f(x)=ax-ln(-x)有最小值是3,
则
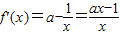
(ⅰ)当a=0,x∈[-e,0)时,
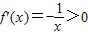
.f(x)在区间[-e,0)上单调递增,
f(x)
min=f(-e)=-1,不满足最小值是3
(ⅱ)当a>0,x∈[-e,0)时,f'(x)>0,f(x)在区间[-e,0)上单调递增,
f(x)
min=f(-e)=-ae-1<0,也不满足最小值是3
(ⅲ)当
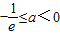
,由于x∈[-e,0),则
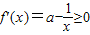
,
故函数f(x)=ax-ln(-x)是[-e,0)上的增函数.
∴f(x)
min=f(-e)=-ae-1=3,解得
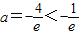
(舍去)
(ⅳ)当
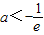
时,则
当

时,
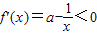
,此时函数f(x)=ax-ln(-x)是减函数;
当
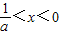
时,
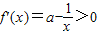
,此时函数f(x)=ax-ln(-x)是增函数.
∴
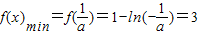
,解得a=-e
2综上可知,存在实数a=-e
2,使得当x∈[-e,0)时,f(x)有最小值3.
点评:本题是一道综合题,考查了利用函数的奇偶性求函数的解析式;构造函数再求其导函数求函数最值证明不等式成立问题;对含有参数用分类讨论思想判断导函数的符号再求出函数的最值,本题综合性强且计算量大,应是难度很大的题.

 ,求证:当a=-1时,
,求证:当a=-1时, ;
;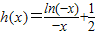 ,分别求出这两个函数的导函数和符号,判断出它们在区间[-e,0)的单调性,并求出f(x)的最小值和h(x)的最大值,判断出最小值比最大值大,则不等式成立;
,分别求出这两个函数的导函数和符号,判断出它们在区间[-e,0)的单调性,并求出f(x)的最小值和h(x)的最大值,判断出最小值比最大值大,则不等式成立;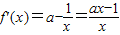 ,对a的符号分类讨论来确定f'(x)的符号,进而判断出在区间[-e,0)上的单调性,求出最小值和m的值,注意验证范围是否符合.
,对a的符号分类讨论来确定f'(x)的符号,进而判断出在区间[-e,0)上的单调性,求出最小值和m的值,注意验证范围是否符合.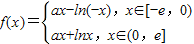
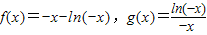 ,
,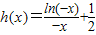 ,
,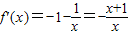 ,
,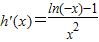 ,
,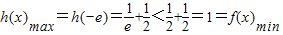
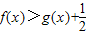
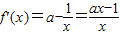
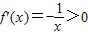 .f(x)在区间[-e,0)上单调递增,
.f(x)在区间[-e,0)上单调递增,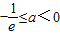 ,由于x∈[-e,0),则
,由于x∈[-e,0),则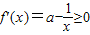 ,
,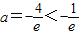 (舍去)
(舍去)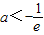 时,则
时,则 时,
时,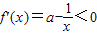 ,此时函数f(x)=ax-ln(-x)是减函数;
,此时函数f(x)=ax-ln(-x)是减函数;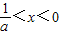 时,
时,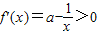 ,此时函数f(x)=ax-ln(-x)是增函数.
,此时函数f(x)=ax-ln(-x)是增函数.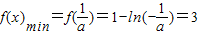 ,解得a=-e2
,解得a=-e2

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案 已知函数f(x)=x+
已知函数f(x)=x+