
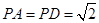 ,
,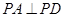 ,底面
,底面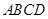 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD, 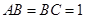 ,O为AD中点.
,O为AD中点.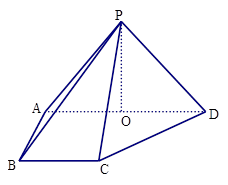
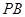 与平面
与平面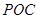 所成角的余弦值;
所成角的余弦值;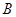 点到平面
点到平面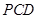 的距离;
的距离;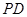 上是否存在一点
上是否存在一点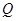 ,使得二面角
,使得二面角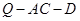 的余弦值为
的余弦值为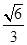 ?若存在,求出
?若存在,求出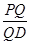 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.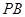 与平面
与平面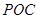 所成角的余弦值为
所成角的余弦值为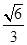 ;(2)
;(2) 点到平面
点到平面 的距离
的距离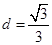 ;(3)存在,
;(3)存在,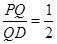 .
. 中,易得
中,易得 所以可以
所以可以 为坐标原点,
为坐标原点, 为
为 轴,
轴, 为
为 轴,
轴, 为
为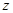 轴建立空间直角坐标系,然后利用空间向量求解. 思路二、(1)易得
轴建立空间直角坐标系,然后利用空间向量求解. 思路二、(1)易得 平面
平面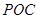 ,所以
,所以 即为所求.(2)由于
即为所求.(2)由于 ,从而
,从而 平面
平面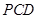 ,所以可转化为求点
,所以可转化为求点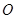 到平面
到平面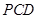 .(3)假设存在,过Q作
.(3)假设存在,过Q作 ,垂足为
,垂足为 ,过
,过 作
作 ,垂足为M,则
,垂足为M,则 即为二面角
即为二面角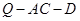 的平面角.设
的平面角.设 ,利用
,利用 求出
求出 ,若
,若 ,则存在,否则就不存在.
,则存在,否则就不存在.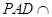 平面ABCD="AD,"
平面ABCD="AD,"  平面PAD,
平面PAD,
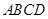 中,易得
中,易得 ;
;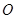 为坐标原点,
为坐标原点, 为
为 轴,
轴, 为
为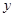 轴,
轴, 为
为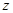 轴建立空间直角坐标系.
轴建立空间直角坐标系. ,
, ,
,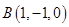
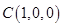 ,
, ;
;
 ,易证:
,易证: ,
, 平面
平面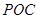 的法向量,
的法向量, 
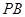 与平面
与平面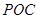 所成角的余弦值为
所成角的余弦值为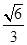 .4分
.4分 ,设平面PDC的法向量为
,设平面PDC的法向量为 ,
, ,取
,取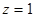 得
得
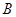 点到平面
点到平面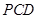 的距离
的距离 .8分
.8分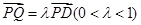 .
.
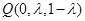 ,
, ,则
,则
 ,得
,得 .
. ,
,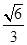 ,所以
,所以
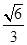 .
. 或
或 (舍去),
(舍去),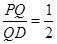 13分
13分

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:不详 题型:解答题
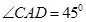 .
.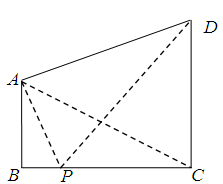
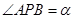 ,
,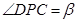 ,问点P在何处时,
,问点P在何处时,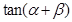 最小?
最小?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
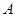 在平面
在平面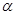 内,其余顶点在
内,其余顶点在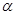 的同侧,正方体上与顶点
的同侧,正方体上与顶点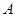 相邻的三个顶点到
相邻的三个顶点到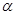 的距离分别为1,2和4,
的距离分别为1,2和4,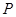 是正方体的其余四个顶点中的一个,则
是正方体的其余四个顶点中的一个,则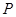 到平面
到平面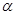 的距离可能是:
的距离可能是: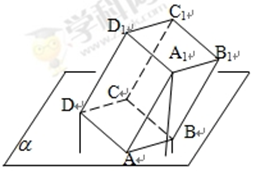
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com