
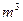 ,深为3
,深为3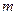 .如果池底每平方米的造价为150元,池壁每平方米的造价为
.如果池底每平方米的造价为150元,池壁每平方米的造价为 120元,怎样设计水池能使总造价最低?最低造价是多少?
120元,怎样设计水池能使总造价最低?最低造价是多少? 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源:不详 题型:解答题
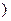 ,每人每年可创利10万元.据评估,在经营条件不变的前提下,若裁员x人,则留岗职员每人每年多创利0.1x万元,但公司需付下岗职员每人每年4万元的生活费,并且该公司正常运转情况下,所裁人数不超过50人,为获得最大的经济效益,该公司应裁员多少人?
,每人每年可创利10万元.据评估,在经营条件不变的前提下,若裁员x人,则留岗职员每人每年多创利0.1x万元,但公司需付下岗职员每人每年4万元的生活费,并且该公司正常运转情况下,所裁人数不超过50人,为获得最大的经济效益,该公司应裁员多少人?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
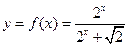 上两点
上两点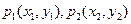 ,若
,若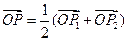 ,且P点的横坐标为
,且P点的横坐标为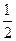 .
. 标;
标;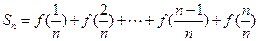 求
求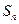 ;
;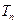 为数列
为数列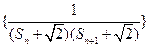 的前n项和,若
的前n项和,若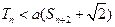 对一切
对一切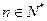 都成立,试求a的取值范围.
都成立,试求a的取值范围. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com