
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .数列
.数列![]() 满足
满足![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用![]() 与
与![]() 的关系作差可知数列
的关系作差可知数列![]() 为等差数列与公差,即可求得通项公式;
为等差数列与公差,即可求得通项公式;
(2)由(1)表示数列![]() 的通项公式,由裂项相消法求和即可;
的通项公式,由裂项相消法求和即可;
(3)分类讨论![]() 为偶数与奇数时转化不等式,再由基本不等式与函数的单调性求最值,最后由不等式恒成立问题转化求参数取值范围即可.
为偶数与奇数时转化不等式,再由基本不等式与函数的单调性求最值,最后由不等式恒成立问题转化求参数取值范围即可.
解:(1)当![]() 时,
时,![]() ;
;
当![]() 时,因为
时,因为![]() ,
,![]() ,所以
,所以![]() ,
,
两式相减得![]() ,
,
所以![]() ,所以数列
,所以数列![]() 是以1为首项,2为公差的等差数列,
是以1为首项,2为公差的等差数列,
所以![]() .
.
(2)由题意和(1)得:![]() ,
,
所以数列![]() 前
前![]() 项和
项和![]() .
.
(3)①当![]() 为偶数时,要使不等式
为偶数时,要使不等式![]() 恒成立,即不等式
恒成立,即不等式![]() 恒成立,即需不等式
恒成立,即需不等式![]() 恒成立.
恒成立.
∵![]() ,等号在
,等号在![]() 时取得.
时取得.
![]() 此时
此时![]() 需满足
需满足![]() .
.
②当![]() 为奇数时,要使不等式
为奇数时,要使不等式![]() 恒成立,即不等式
恒成立,即不等式![]() 恒成立,即需不等式
恒成立,即需不等式![]() 恒成立.
恒成立.
∵![]() 是随
是随![]() 的增大而增大,
的增大而增大,
∴![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
![]() 此时
此时![]() 需满足
需满足![]() .
.
综合①、②可得![]() 的取值范围是
的取值范围是![]() .
.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
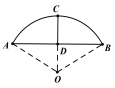
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() ,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为
,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为![]() ,半径等于4米的弧田.下列说法不正确的是( )
,半径等于4米的弧田.下列说法不正确的是( )
A. “弦”![]() 米,“矢”
米,“矢”![]() 米
米
B. 按照经验公式计算所得弧田面积(![]() )平方米
)平方米
C. 按照弓形的面积计算实际面积为(![]() )平方米
)平方米
D. 按照经验公式计算所得弧田面积比实际面积少算了大约0.9平方米(参考数据![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)若函数![]() 在
在![]() 上是增函数,求正数
上是增函数,求正数![]() 的取值范围;
的取值范围;
(2)当![]() 时,设函数
时,设函数![]() 的图象与x轴的交点为
的图象与x轴的交点为![]() ,
,![]() ,曲线
,曲线![]() 在
在![]() ,
,![]() 两点处的切线斜率分别为
两点处的切线斜率分别为![]() ,
,![]() ,求证:
,求证:![]() +
+![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知4名学生和2名教师站在一排照相,求:
(1)中间二个位置排教师,有多少种排法?
(2)首尾不排教师,有多少种排法?
(3)两名教师不站在两端,且必须相邻,有多少种排法?
(4)两名教师不能相邻的排法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为常数,函数
为常数,函数![]() .
.
(1)当![]() 时,求关于
时,求关于![]() 的不等式
的不等式![]() 的解集;
的解集;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)对于给定的![]() ,且
,且![]() ,
,![]() ,证明:关于
,证明:关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有一个实数根.
内有一个实数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在边长为60 cm的正方形铁片的四角上切去相等的正方形,再把它沿虚线折起,做成一个无盖的长方体箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理是合情推理的是( )
①由圆的性质类比出球的有关性质;
②由直角三角形、等腰三角形、等边三角形内角和是![]() 归纳出所有三角形的内角和都是
归纳出所有三角形的内角和都是![]() ;③由
;③由![]() ,满足
,满足![]() ,
,![]() ,推出
,推出![]() 是奇函数;
是奇函数;
④三角形内角和是![]() ,四边形内角和是
,四边形内角和是![]() ,五边形内角和是
,五边形内角和是![]() ,由此得凸多边形内角和是
,由此得凸多边形内角和是![]() .
.
A. ①②B. ①③④C. ②④D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个不共线的向量![]() ,
,![]() 夹角为
夹角为![]() ,且
,且![]() ,
,![]() ,为正实数.
,为正实数.
(1)若![]() 与
与![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最小值及对应的x的值,并指出此时向量
的最小值及对应的x的值,并指出此时向量![]() 与
与![]() 的位置关系.
的位置关系.
(3)若![]() 为锐角,对于正实数m,关于x的方程
为锐角,对于正实数m,关于x的方程![]() 两个不同的正实数解,且
两个不同的正实数解,且![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com