
【题目】已知![]() ,
,![]() 为常数,函数
为常数,函数![]() .
.
(1)当![]() 时,求关于
时,求关于![]() 的不等式
的不等式![]() 的解集;
的解集;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)对于给定的![]() ,且
,且![]() ,
,![]() ,证明:关于
,证明:关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有一个实数根.
内有一个实数根.
【答案】(1)当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() 或
或![]() ;当
;当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ;当
;当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() 或
或![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)当![]() 时,
时,![]() ,分
,分![]() ,
,![]() ,
,![]() 三种情况讨论,求不等式
三种情况讨论,求不等式![]() 的解集;
的解集;
(2)当![]() 时,
时,![]() ,其图象的对称轴为
,其图象的对称轴为![]() .分
.分![]() ,
,![]() ,
,![]() 三种情况讨论,即求实数
三种情况讨论,即求实数![]() 的取值范围;
的取值范围;
(3)设![]() .由
.由![]() ,得
,得![]() .对于给定的
.对于给定的![]() ,且
,且![]() ,
,![]() ,得
,得![]() 在区间
在区间![]() 上单调,故
上单调,故![]() 在区间
在区间![]() 上有且只有一个零点,即方程
上有且只有一个零点,即方程![]() 在区间
在区间![]() 内有一个实数根.
内有一个实数根.
(1)当![]() 时,
时,![]() .
.
当![]() ,即
,即![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
![]() 不等式
不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,![]() 不等式
不等式![]() 的解集为
的解集为![]() .
.
当![]() ,即
,即![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,
,
![]() 不等式
不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
综上,当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() 或
或![]() ;
;
当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() ;
;
当![]() 时,不等式
时,不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(2)当![]() 时,
时,![]() ,其图象的对称轴为
,其图象的对称轴为![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
![]() 在
在![]() 上存在零点,
上存在零点,![]() ,即得
,即得![]() .
.
![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上存在零点,
上存在零点,
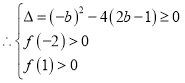 或
或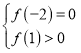 或
或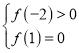 或
或![]() ,
,
解得![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() .
.
![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
![]() 在
在![]() 上存在零点,
上存在零点,![]() ,即得
,即得![]() .
.
![]() .
.
综上,![]() .
.
![]() 实数
实数![]() 的取值范围为
的取值范围为![]() .
.
(3)设![]() .
.
当![]() 给定时,
给定时,![]() 为定值.
为定值.
![]() ,
,
![]() .
.
又对于给定的![]() ,且
,且![]() ,
,![]() ,
,
![]() 在区间
在区间![]() 上单调,即
上单调,即![]() 在区间
在区间![]() 上单调,
上单调,
![]() 在区间
在区间![]() 上有且只有一个零点,
上有且只有一个零点,
即方程![]() 在区间
在区间![]() 内有一个实数根.
内有一个实数根.


科目:高中数学 来源: 题型:
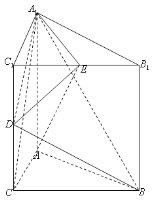
【题目】已知三棱柱![]() 中,三个侧面均为矩形,底面
中,三个侧面均为矩形,底面![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上运动.
上运动.
(1)求证![]()
![]()
![]() ;
;
(2)当点![]() 运动到某一位置时,恰好使二面角
运动到某一位置时,恰好使二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离;
的距离;
(3)在(2)的条件下,试确定线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)试探究函数![]() 在定义域内是否存在零点,若存在,请指出有几个零点;若不存在,请说明理由;
在定义域内是否存在零点,若存在,请指出有几个零点;若不存在,请说明理由;
(Ⅲ)若![]() ,且
,且![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
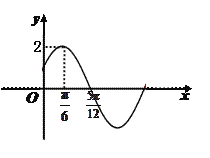
(1) 求函数![]() 的解析式;
的解析式;
(2) 如何由函数![]() 的通过适当图象的变换得到函数
的通过适当图象的变换得到函数![]() 的图象, 写出变换过程;
的图象, 写出变换过程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .数列
.数列![]() 满足
满足![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】牡丹江一中2019年将实行新课程改革,即除语、数、外三科为必考科目外,还要在理、化、生、史、地、政六科中选择三科作为选考科目.已知某生的高考志愿为北京大学环境科学专业,按照17年北大高考招生选考科目要求物、化必选,为该生安排课表(上午四节、下午四节,上午第四节和下午第一节不算相邻),现该生某天最后两节为自习课,且数学不排下午第一节,语文、外语不相邻,则该生该天课表有( )种.
A. 444B. 1776C. 1440D. 1560
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某早餐店对一款新口味的酸奶进行了一段时间试销,定价为5元/瓶.酸奶在试销售期间足量供应,每天的销售数据按照[15,25],(25,35],(35,45],(45,55]分组,得到如下频率分布直方图,以不同销量的频率估计概率.试销结束后,这款酸奶正式上市,厂家只提供整箱批发:大箱每箱50瓶,批发成本85元;小箱每箱30瓶,批发成本65元.由于酸奶保质期短,当天未卖出的只能作废.该早餐店以试销售期间的销量作为参考,决定每天仅批发一箱(计算时每个分组取中间值作为代表,比如销量为(45,55]时看作销量为50瓶).

(1)设早餐店批发一大箱时,当天这款酸奶的利润为随机变量X,批发一小箱时,当天这款酸奶的利润为随机变量Y,求X和Y的分布列;
(2)从早餐店的收益角度和利用所学的知识作为决策依据,该早餐店应每天批发一大箱还是一小箱?(必须作出一种合理的选择)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD-A1B1C1D1中,CD∥AB, AB⊥BC,AB=BC=2CD=2,侧棱AA1⊥平面ABCD.且点M是AB1的中点
(1)证明:CM∥平面ADD1A1;
(2)求点M到平面ADD1A1的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com