
【题目】如图,四棱柱ABCD-A1B1C1D1中,CD∥AB, AB⊥BC,AB=BC=2CD=2,侧棱AA1⊥平面ABCD.且点M是AB1的中点
(1)证明:CM∥平面ADD1A1;
(2)求点M到平面ADD1A1的距离.

【答案】(1)见解析(2)![]()
【解析】试题分析:(1)根据题意得到四边形AECD为平行四边形,∴CE∥AD,∴CE∥平面![]() ,进而得到面面平行,再得到线面平行;(2)根据等体积法得到
,进而得到面面平行,再得到线面平行;(2)根据等体积法得到![]() ,列式求得
,列式求得![]() .
.
解析:
(1)取AB的中点E,连结CE、ME.
∵M为AB1的中点 ∴ME∥BB1∥AA1
又∵AA1![]() 平面ADD1A1 ∴ME∥平面ADD1A1
平面ADD1A1 ∴ME∥平面ADD1A1
又∵AB∥CD,CD= ![]() AB ∴AE平行且等于CD ∴四边形AECD为平行四边形 ∴CE∥AD又∵AD
AB ∴AE平行且等于CD ∴四边形AECD为平行四边形 ∴CE∥AD又∵AD![]() 平面ADD1A1 ∴CE∥平面ADD1A1
平面ADD1A1 ∴CE∥平面ADD1A1
又∵ME∩CE=E ∴平面CME∥平面ADD1A1
又∵CM![]() 平面CME ∴CM∥平面ADD1A1
平面CME ∴CM∥平面ADD1A1
(2)由(1)可知CM∥平面ADD1A1,所以M到平面ADD1A1的距离等价于C到平面ADD1A1的距离,不妨设为h,则![]() .
.
![]()
在梯形ABCD中,可计算得AD= ![]() ,
,
则![]()
∴![]() =
= ![]() ,得
,得![]() ,即点M到平面ADD1A1的距离
,即点M到平面ADD1A1的距离![]()


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为常数,函数
为常数,函数![]() .
.
(1)当![]() 时,求关于
时,求关于![]() 的不等式
的不等式![]() 的解集;
的解集;
(2)当![]() 时,若函数
时,若函数![]() 在
在![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(3)对于给定的![]() ,且
,且![]() ,
,![]() ,证明:关于
,证明:关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有一个实数根.
内有一个实数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,它的前
,它的前![]() 项和为
项和为![]() ,
,
(ⅰ)求![]() ;
;
(ⅱ)若存在正整数![]() ,使不等式
,使不等式![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xcos+a,a∈R.
(I)求曲线y=f(x)在点x=![]() 处的切线的斜率;
处的切线的斜率;
(II)判断方程f '(x)=0(f '(x)为f(x)的导数)在区间(0,1)内的根的个数,说明理由;
(III)若函数F(x)=xsinx+cosx+ax在区间(0,1)内有且只有一个极值点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个不共线的向量![]() ,
,![]() 夹角为
夹角为![]() ,且
,且![]() ,
,![]() ,为正实数.
,为正实数.
(1)若![]() 与
与![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的最小值及对应的x的值,并指出此时向量
的最小值及对应的x的值,并指出此时向量![]() 与
与![]() 的位置关系.
的位置关系.
(3)若![]() 为锐角,对于正实数m,关于x的方程
为锐角,对于正实数m,关于x的方程![]() 两个不同的正实数解,且
两个不同的正实数解,且![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
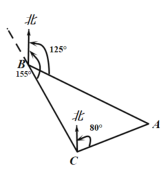
【题目】如图,货轮在海上B处,以50海里/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155o的方向航行,为了确定船位,在B点处观测到灯塔A的方位角为125o.半小时后,货轮到达C点处,观测到灯塔A的方位角为80o.求此时货轮与灯塔之间的距离(答案保留最简根号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述错误的是( )
A.已知直线![]() 和平面
和平面![]() ,若点
,若点![]() ,点
,点![]() 且
且![]() ,
,![]() ,则
,则![]()
B.若三条直线两两相交,则三条直线确定一个平面
C.若直线![]() 不平行于平面
不平行于平面![]() ,且
,且![]() ,则
,则![]() 内的所有直线与
内的所有直线与![]() 都不相交
都不相交
D.若直线![]() 和
和![]() 不平行,且
不平行,且![]() ,
,![]() ,
,![]() ,则l至少与
,则l至少与![]() ,
,![]() 中的一条相交
中的一条相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88,若样本B数据恰好是样本A数据都加上2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A. 众数 B. 平均数
C. 中位数 D. 标准差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com