【题目】下列叙述错误的是（ ）
A.已知直线
和平面
，若点
，点
且
，
，则
B.若三条直线两两相交，则三条直线确定一个平面
C.若直线不平行于平面，且
，则内的所有直线与都不相交
D.若直线
和
不平行，且
，
，
，则l至少与，中的一条相交
科目：高中数学 来源： 题型：
【题目】某早餐店对一款新口味的酸奶进行了一段时间试销，定价为5元/瓶．酸奶在试销售期间足量供应，每天的销售数据按照[15，25]，（25，35]，（35，45]，（45，55]分组，得到如下频率分布直方图，以不同销量的频率估计概率．试销结束后，这款酸奶正式上市，厂家只提供整箱批发：大箱每箱50瓶，批发成本85元；小箱每箱30瓶，批发成本65元．由于酸奶保质期短，当天未卖出的只能作废．该早餐店以试销售期间的销量作为参考，决定每天仅批发一箱（计算时每个分组取中间值作为代表，比如销量为（45，55]时看作销量为50瓶）．
（1）设早餐店批发一大箱时，当天这款酸奶的利润为随机变量X，批发一小箱时，当天这款酸奶的利润为随机变量Y，求X和Y的分布列；
（2）从早餐店的收益角度和利用所学的知识作为决策依据，该早餐店应每天批发一大箱还是一小箱？（必须作出一种合理的选择）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱柱ABCD-A1B1C1D1中，CD∥AB, AB⊥BC,AB=BC=2CD=2,侧棱AA1⊥平面ABCD.且点M是AB1的中点
(1)证明:CM∥平面ADD1A1；
(2)求点M到平面ADD1A1的距离.
查看答案和解析>>
科目：高中数学 来源： 题型：
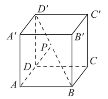
【题目】如图所示,已知点P在正方体ABCD-A′B′C′D′的对角线BD′上,∠PDA=60°.
(1)求DP与CC′所成角的大小.
(2)求DP与平面AA′D′D所成角的大小.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设抛物线
的焦点为
，过点
的直线与抛物线相交于
两点，与抛物线的准线相交于点
， 
，则
与
的面积之比
__________．
【答案】
【解析】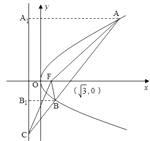
由题意可得抛物线的焦点
的坐标为
，准线方程为
。
如图，设
，过A,B分别向抛物线的准线作垂线，垂足分别为E,N，则
，解得
。
把
代入抛物线
，解得
。
∴直线AB经过点
与点
，
故直线AB的方程为
，代入抛物线方程解得
。
∴
。
在
中， 
，
∴
∴
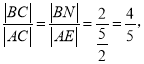
。答案： 
点睛：
在解决与抛物线有关的问题时，要注意抛物线的定义在解题中的应用。抛物线定义有两种用途：一是当已知曲线是抛物线时，抛物线上的点M满足定义，它到准线的距离为d，则|MF|＝d，可解决有关距离、最值、弦长等问题；二是利用动点满足的几何条件符合抛物线的定义，从而得到动点的轨迹是抛物线．
【题型】填空题
【结束】
17
【题目】已知
三个内角
所对的边分别是
，若
.
（1）求角
；
（2）若
的外接圆半径为2，求
周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
