
【题目】在下列命题中:①在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则解三角形只有唯一解的充要条件是:
,则解三角形只有唯一解的充要条件是:![]() ;②当
;②当![]() 时,
时,![]() ;③在
;③在![]() 中,若
中,若![]() ,则
,则![]() 中一定为钝角三角形;④扇形圆心角
中一定为钝角三角形;④扇形圆心角![]() 为锐角,周长为定值,则它面积最大时,一定有
为锐角,周长为定值,则它面积最大时,一定有![]() ;⑤函数
;⑤函数![]() 的单增区间为
的单增区间为![]() ,其中真命题的序号为_____.
,其中真命题的序号为_____.
【答案】①②③⑤;
【解析】
对每一个命题逐一分析判断得解. ①,利用正弦定理分析判断;②,利用反三角函数的图象分析判断;③,利用反证法判断;④,利用基本不等式判断得解;⑤,利用复合函数的单调性分析求解.
①,由正弦定理得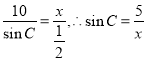 ,因为三角形有唯一解,所以
,因为三角形有唯一解,所以![]() 或
或![]() ,所以该命题正确;
,所以该命题正确;
②,画图得

当![]() 时,
时,![]() ,所以该命题是真命题;
,所以该命题是真命题;
③假设△ABC是锐角三角形,![]() ,
,
所以![]() ,显然矛盾;假设△ABC是直角三角形,显然A,B不可能是直角,所以C是直角,此时
,显然矛盾;假设△ABC是直角三角形,显然A,B不可能是直角,所以C是直角,此时![]() ,与已知矛盾,所以
,与已知矛盾,所以![]() 中一定为钝角三角形,所以该命题是真命题;
中一定为钝角三角形,所以该命题是真命题;
④,设扇形的半径为![]() ,扇形圆心角
,扇形圆心角![]() 为锐角,弧长为
为锐角,弧长为![]() ,周长
,周长![]() 为定值,则它面积
为定值,则它面积![]() ,当且仅当
,当且仅当![]() 即
即![]() 时取最大值,但是
时取最大值,但是![]() ,不是锐角,所以该命题不正确;
,不是锐角,所以该命题不正确;
⑤,因为函数![]() 是一个减函数,所以函数
是一个减函数,所以函数![]() 的单增区间为
的单增区间为![]() 的减区间
的减区间![]() ,所以该命题是真命题.
,所以该命题是真命题.
故答案为:①②③⑤


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() :
:![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,椭圆
,椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() .试判断
.试判断![]() 是否为定值?若是求出该定值,若不是定值,请说明理由.
是否为定值?若是求出该定值,若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥
中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥![]() 的体积为
的体积为![]()
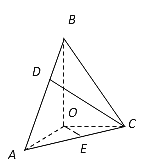
(1)求三棱锥![]() 的高;
的高;
(2)在线段AB上取一点D,当D在什么位置时,![]() 和
和![]() 的夹角大小为
的夹角大小为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为两非零有理数列(即对任意的
为两非零有理数列(即对任意的![]() ,
,![]() 均为有理数),
均为有理数),![]() 为一无理数列(即对任意的
为一无理数列(即对任意的![]() ,
,![]() 为无理数).
为无理数).
(1)已知![]() ,并且
,并且![]() 对任意的
对任意的![]() 恒成立,试求
恒成立,试求![]() 的通项公式.
的通项公式.
(2)若![]() 为有理数列,试证明:对任意的
为有理数列,试证明:对任意的![]() ,
,![]() 恒成立的充要条件为
恒成立的充要条件为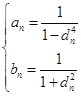 .
.
(3)已知![]() ,
,![]() ,对任意的
,对任意的![]() ,
,![]() 恒成立,试计算
恒成立,试计算![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 过点
过点![]() ,焦点
,焦点![]() ,圆
,圆![]() 的直径为
的直径为![]() .
.
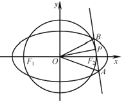
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.若
两点.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)令![]() ,已知函数
,已知函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若存在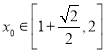 ,使不等式
,使不等式![]() 对任意
对任意![]() (取值范围内的值)恒成立,求实数
(取值范围内的值)恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com