
【题目】设函数![]() ,
,![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,求
轴平行,求![]() ;
;
(2)当![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 轴上方,求
轴上方,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)a=e;(Ⅱ)a的最大值为2e;
【解析】
(Ⅰ)先求导数,再根据导数几何意义得切线斜率,最后根据条件列方程解得a;(Ⅱ)先求导数,再根据导函数零点与1大小分类讨论,根据函数单调性确定函数最小值,最后根据最小值大于零,解得a的取值范围,即得最大值.
(Ⅰ)∵![]() ,∴f'(x)=ex
,∴f'(x)=ex![]() a,∴f'(1)=e
a,∴f'(1)=e![]() a,
a,
由题设知f'(1)=0,即e![]() a=0,解得a=e.
a=0,解得a=e.
经验证a=e满足题意.
(Ⅱ)令f'(x)=0,即ex=a,则x=lna,
(1)当lna<1时,即0<a<e
对于任意x∈(-∞,lna)有f'(x)<0,故f(x)在(-∞,lna)单调递减;
对于任意x∈(lna,1)有f'(x)>0,故f(x)在(lna,1)单调递增,
因此当x=lna时,f(x)有最小值为![]() 成立.所以0<a<e,
成立.所以0<a<e,
(2)当lna≥1时,即a≥e对于任意x∈(-∞,1)有f'(x)<0,
故f(x)在(-∞,1)单调递减,所以f(x)>f(1).
因为f(x)的图象恒在x轴上方,所以f(1)≥0,即a≤2e,
综上,a的取值范围为(0,2e],所以a的最大值为2e.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线![]() 与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(I)求接受甲种心理暗示的志愿者中包含A1但不包含![]() 的频率。
的频率。
(II)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,点A(x1,y1)和点B(x2,y2)是单位圆x2+y2=1上两点,|AB|=1,则∠AOB=______;|y1+2|+|y2+2|的最大值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有下列四个命题:
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :“
:“![]() ”是“
”是“![]() 为奇函数”的充要条件;
为奇函数”的充要条件;
![]() :“等比数列
:“等比数列![]() 中,
中,![]() ”是“等比数列
”是“等比数列![]() 是递减数列”的充要条件.
是递减数列”的充要条件.
其中,真命题的是![]()
![]()
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,过
,过![]() 点作
点作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,
,![]() .连结
.连结![]() ,交
,交![]() 于点
于点![]() ,如图1,将
,如图1,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 到达点
到达点![]() 的位置,如图2.
的位置,如图2.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一长为100码,宽为80码,球门宽为8码的矩形足球运动场地,如图所示,其中![]() 是足球场地边线所在的直线,球门
是足球场地边线所在的直线,球门![]() 处于所在直线的正中间位置,足球运动员(将其看做点
处于所在直线的正中间位置,足球运动员(将其看做点![]() )在运动场上观察球门的角
)在运动场上观察球门的角![]() 称为视角.
称为视角.
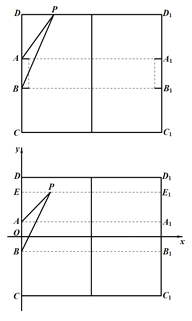
(1)当运动员带球沿着边线![]() 奔跑时,设
奔跑时,设![]() 到底线的距离为
到底线的距离为![]() 码,试求当
码,试求当![]() 为何值时
为何值时![]() 最大;
最大;
(2)理论研究和实践经验表明:张角![]() 越大,射门命中率就越大.现假定运动员在球场都是沿着垂直于底线的方向向底线运球,运动到视角最大的位置即为最佳射门点,以
越大,射门命中率就越大.现假定运动员在球场都是沿着垂直于底线的方向向底线运球,运动到视角最大的位置即为最佳射门点,以![]() 的中点为原点建立如图所示的直角坐标系,求在球场区域
的中点为原点建立如图所示的直角坐标系,求在球场区域![]() 内射门到球门
内射门到球门![]() 的最佳射门点的轨迹.
的最佳射门点的轨迹.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com