
���� ����ֱ��l�ļ����귽�̻�Ϊ��cos��-��sin��-1=0����x=��cos�ȣ�y=��sin�ȣ������ֱ��l����ͨ���̣�����C�IJ���������ȥ�������������C����ͨ���̣�
����M��ֱ������Ϊ��1��0������M��ֱ��l�ϣ����ֱ��l�IJ������̣��õ�${t}^{2}-4\sqrt{2}t-8=0$���ɴ�����Τ�ﶨ�������$\frac{1}{|MA|}+\frac{1}{|MB|}$��ֵ��
��� �⣺������Ϊ$\sqrt{2}\;��cos����+\frac{��}{4}��-1=0$��
���Ԧ�cos��-��sin��-1=0
��x=��cos�ȣ�y=��sin�ȣ�
��x-y-1=0����3�֣�
��Ϊ$\left\{\begin{array}{l}x=4{t^2}\\ y=4t\end{array}\right.$��ȥt��y2=4x��
����ֱ��l������C����ͨ���̷ֱ�Ϊx-y-1=0��y2=4x������4�֣�
����M��ֱ������Ϊ��1��0������M��ֱ��l�ϣ�
��ֱ��l�IJ������̣�$\left\{\begin{array}{l}x=1+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$��tΪ��������A��B��Ӧ�IJ���Ϊt1��t2��
${t}^{2}-4\sqrt{2}t-8=0$��
${t}_{1}+{t}_{2}=4\sqrt{2}��{t}_{1}{t}_{2}=-8$������7�֣�
��$\frac{1}{|MA|}+\frac{1}{|MB|}$=$\frac{|{t}_{1}-{t}_{2}|}{|{t}_{1}{t}_{2}|}$=$\frac{\sqrt{��{t}_{1}+{t}_{2}��^{2}-4{t}_{1}{t}_{2}}}{|{t}_{1}{t}_{2}|}$=$\frac{\sqrt{32+32}}{8}$=1������10�֣�
���� ��С����Ҫ����������̡�������Ȼ���֪ʶ��������������������������ν��˼�롢������ת��˼�룬���е��⣮


 �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{5}{12}$ | C�� | $\frac{4}{5}$ | D�� | $\frac{5}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
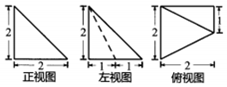 ijһ�ռ伸���������ͼ��ͼ��ʾ����ü��������ⳤΪ��������
ijһ�ռ伸���������ͼ��ͼ��ʾ����ü��������ⳤΪ��������| A�� | 2 | B�� | $\sqrt{5}$ | C�� | 2$\sqrt{2}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
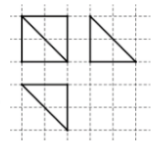 ��ͼ������ֽ��С�����εı߳�Ϊ1������������ij�����������ͼ����˼��������ֱ�������εĸ����ǣ�������
��ͼ������ֽ��С�����εı߳�Ϊ1������������ij�����������ͼ����˼��������ֱ�������εĸ����ǣ�������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2}$+$\frac{3}{2}$i | B�� | $\frac{1}{2}$+$\frac{3}{2}$i | C�� | -$\frac{1}{2}$-$\frac{3}{2}$i | D�� | $\frac{1}{2}$-$\frac{3}{2}$i |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com