考点:综合法与分析法(选修),基本不等式
专题:不等式的解法及应用
分析:本题涉及基本不等式,需要构造三元函数,经过特殊化处理后,转化为二元函数,再通过换元,得到一元函数,求出导函数研究最值,得到本题的解.
解答:
解:设三元函数
f(a,b,c)=++,
当a=b=c=1时,
f(a,b,c)=≥.原命题成立.
∵a,b,c∈R
+,abc=1,
∴a、b、c中至少有一个不大于1.
不妨设b≤1.
f(a,b,c)-f(a,1,c)=++-[++]=
++≥0
∴f(a,b,c)≥f(a,1,c).
要证
f(a,b,c)≥,只要证
f(a,1,c)≥.
此时,ac=1,设
a=,c=q(q>0).
f(a,1,c)=++=
++=
+∵q
5-1=(q+1)(q
4-q
3+q
2-q+1)
∴
f(q,1,c)=q2-q+1-++=
(q+)2-(q+)+-1设
t=q+,
g(t)=t2-t+-1.
∵t≥2,
∴
g′(t)=2t+1-=>0,
∴g(t)在[2,+∞)单调递增.
∴
g(t)≥g(2)=.
故
f(a,b,c)≥f(a,1,c)≥.
原命题得证.
点评:本题构造了三元函数,通过化归转化,最后得到了一元函数,利用导函数,求出最值,得到本题结论.本题思维要求高,运算难度大,属于难题.



 阅读快车系列答案
阅读快车系列答案 如图,已知A1,A2,B1,B2分别是椭圆C:
如图,已知A1,A2,B1,B2分别是椭圆C:
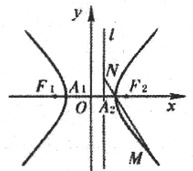 如图,A1、A2、F1、F2分别是双曲线C:
如图,A1、A2、F1、F2分别是双曲线C:
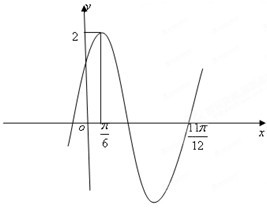 已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<
已知函数f(x)=Asin(wx+φ)(A>0,W>0,|φ|<