考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)直线MA
2方程为:y
0(x-3)-(x
0-3)y=0,代入双曲线方程,能求出点N的轨迹E的方程.
(2)设
B(3cosθ,4sinθ)(0<θ<),则直线F
1B的方程为:
y=(x+5),由此入手能证明点G在双曲线C的左准线
x=-上.
解答:
(本小题满分13分)
(1)解:直线MA
2方程为:y
0(x-3)-(x
0-3)y=0
由方程组
…(2分)
代入双曲线方程化简得:
点N的轨迹E的方程为:
+=1…(5分)
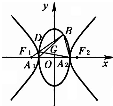
(2)证明:如图,设
B(3cosθ,4sinθ)(0<θ<),
则直线F
1B的方程为:
y=(x+5)代入E的方程化简得:
(17+15cosθ)x
2+(45sin
2θ)x-9cosθ(17cosθ+15)=0…(9分)
∴
xD=-| 9cosθ(17cosθ+15) |
| xB(17+15cosθ) |
=-,
yD=,
∴A
1B的方程为:4sinθ(x+3)-3(cosθ+1)y=0①
A
2D的方程为:sinθ(x-3)+3(cosθ+1)y=0②…(11分)
由①②消去y得:
x=-即点G在双曲线C的左准线
x=-上.…(13分)
点评:本题考查点的轨迹方程的求法,考查点的坐标在双曲线的左准线上的证明,解题时要认真审题,注意函数与方程思想的合理运用.

 如图,A1、A2、F1、F2分别是双曲线C:
如图,A1、A2、F1、F2分别是双曲线C:


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案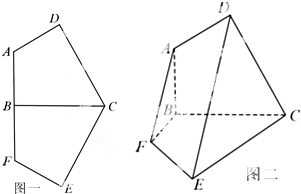 已知轴对称平面五边形ADCEF(如图1),BC为对称轴,AD⊥CD,AD=AB=1,CD=BC=
已知轴对称平面五边形ADCEF(如图1),BC为对称轴,AD⊥CD,AD=AB=1,CD=BC= 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AB⊥AD,平面PAD⊥平面ABCD,若AB=8,DC=2,AD=6
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,AB⊥AD,平面PAD⊥平面ABCD,若AB=8,DC=2,AD=6