Question

已知函数f（x）=e^-x+lnx（e是自然对数的底数），若实数x₀是方程f（x）=0的解，且0＜x₁＜x₀＜x₂，则f（x₁）________f（x₂）（填“＞”，“≥”，“＜”，“≤”）．

Answer 1

＜
分析：先对函数f（x）=e^-x+lnx进行求导，判定在定义域上的单调性，根据单调性即可比较f（x₁），f（x₂）的大小关系．
解答：f’（x）==
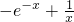
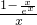
∵x＞0，
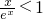
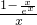
∴f’（x）=＞0则函数f（x）在（0，+∞）上单调递增函数
∵0＜x₁＜x₀＜x₂，
∴f（x₁）＜f（x₂），
故填＜．
点评：本题主要考查了函数与方程的综合运用，以及函数的单调性的应用，属于基础题．