
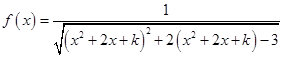 ,其中
,其中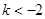 .
. 的定义域
的定义域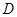 (用区间表示);
(用区间表示); 在
在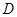 上的单调性;
上的单调性;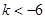 ,求
,求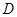 上满足条件
上满足条件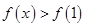 的
的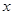 的集合(用区间表示).
的集合(用区间表示).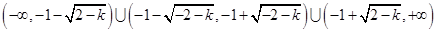 ;
;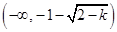 ,
,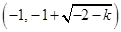 ,
,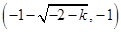 ,
,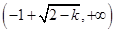 ;
;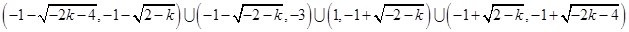 .
.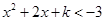 或
或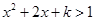 ,对上述两个不等式进行求解,并比较端点值的大小,从而求出函数
,对上述两个不等式进行求解,并比较端点值的大小,从而求出函数 的定义域
的定义域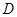 ;(2)求导
;(2)求导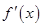 ,并求出方程
,并求出方程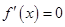 的根,求出不等式
的根,求出不等式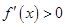 的解集,并与定义域取交集得到函数
的解集,并与定义域取交集得到函数 的单调递增区间,用同样的办法求出函数
的单调递增区间,用同样的办法求出函数 的单调递减区间,但需注意比较各端点值得大小;(3)先求出方程
的单调递减区间,但需注意比较各端点值得大小;(3)先求出方程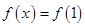 的解,然后结合函数
的解,然后结合函数 的单调性以及函数
的单调性以及函数 的定义域得到不等式
的定义域得到不等式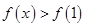 的解集合.
的解集合.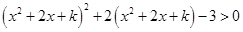 ,
,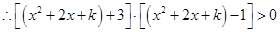 ,
,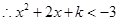 或
或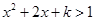 ,
,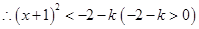 或
或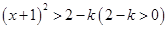 ,
,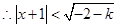 或
或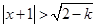 ,
,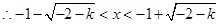 或
或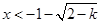 或
或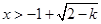 ,
, 的定义域
的定义域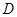 为
为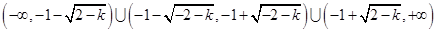 ;
;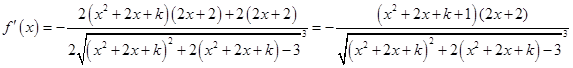 ,
,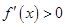 得
得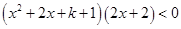 ,即
,即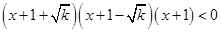 ,
,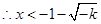 或
或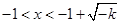 ,结合定义域知
,结合定义域知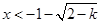 或
或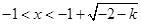 ,
, 的单调递增区间为
的单调递增区间为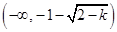 ,
,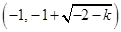 ,
,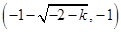 ,
,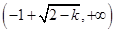 ;
;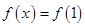 得
得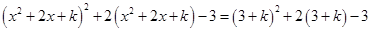 ,
,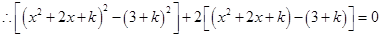 ,
,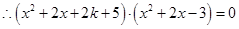 ,
,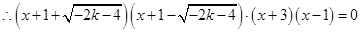 ,
,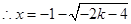 或
或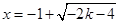 或
或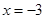 或
或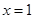 ,
,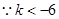 ,
,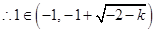 ,
,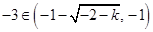 ,
,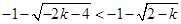 ,
,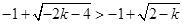 ,
, 的单调性知
的单调性知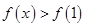 的解集为
的解集为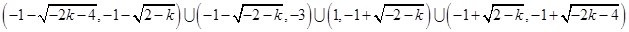 .
.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源:不详 题型:单选题
| 1 |
| 2 |
| A.f′(x)+f(x)=-sinx | B.f′(x)+f(x)=-cosx |
| C.f′(x)-f(x)=sinx | D.f′(x)-f(x)=cosx |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
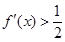 ,则满足
,则满足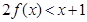 的x的集合为( )
的x的集合为( )| A.{x|x<1} | B.{x|-1<x<1} | C.{x|x<-1或x>1} | D.{x|x>1} |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
|
设函数 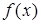 在R上可导,其导函数为 在R上可导,其导函数为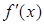 且函数 且函数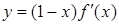 的图像如图所示,则下列结论一定成立的是( ) 的图像如图所示,则下列结论一定成立的是( )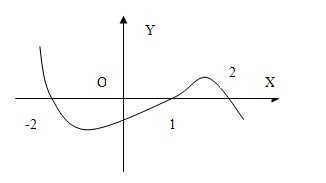
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.{x|x>0} |
| B.{x|x<0} |
| C.{x|x<-1或x>1} |
| D.{x|x<-1或0<x<1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com