
已知函数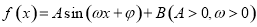 的一系列对应值如下表:
的一系列对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格提供的数据求函数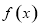 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数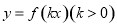 周期为
周期为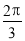 ,当
,当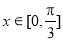 时,
时,
方程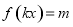 恰有两个不同的解,求实数
恰有两个不同的解,求实数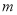 的取值范围.
的取值范围.
(1) ;(2)实数
;(2)实数 的取值范围为
的取值范围为 .
.
【解析】
试题分析:(1)根据表格提供的数据,求出周期T,注意:三角函数的周期等于图象上相邻两个最低点的横坐标之差的绝对值,解出ω,由A>0知函数的最大值为A+B,最小值为-A+B,利用已知最小值、最大值可求出A、B,结合周期求出φ,可求函数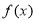 的一个解析式.
的一个解析式.
(2)函数 (k>0)周期为
(k>0)周期为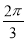 ,求出k,x∈[0,
,求出k,x∈[0,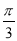 ],推出3x?
],推出3x?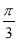 的范围,画出图象,数形结合容易求出m的范围.
的范围,画出图象,数形结合容易求出m的范围.
试题解析:(1)设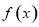 的最小正周期为
的最小正周期为 ,得
,得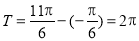 , 2分
, 2分
由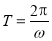 , 得
, 得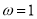 ,又
,又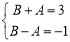 ,解得
,解得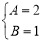 4分
4分
令 ,即
,即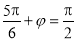 ,解得
,解得 , 5分
, 5分
∴ 6分
6分
(2)∵函数 的周期为
的周期为 ,
,
又 , ∴
, ∴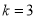 , 7分
, 7分
令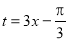 ,∵
,∵ , ∴
, ∴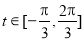 , .8分
, .8分
如图, 在
在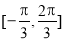 上有两个不同的解,则
上有两个不同的解,则 , 10分
, 10分
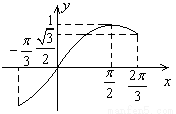
∴方程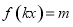 在
在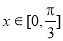 时恰好有两个不同的解,
时恰好有两个不同的解,
则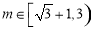 ,即实数
,即实数 的取值范围是
的取值范围是 12分
12分
考点:1.由三角函数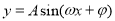 的部分图象求解析式;2.三角函数的周期性及求法.
的部分图象求解析式;2.三角函数的周期性及求法.


科目:高中数学 来源:2016届浙江省高一上学期期中考试数学试卷(解析版) 题型:选择题
已知函数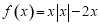 ,则下列结论正确的是( ).
,则下列结论正确的是( ).
A.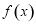 是偶函数,递增区间是
是偶函数,递增区间是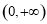
B.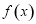 是偶函数,递减区间是
是偶函数,递减区间是
C.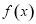 是奇函数,递减区间是
是奇函数,递减区间是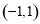
D.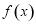 是奇函数,递增区间是
是奇函数,递增区间是
查看答案和解析>>
科目:高中数学 来源:2016届浙江省等三校高一下学期第二次联考数学试卷(解析版) 题型:选择题
在△ABC中,若三个内角A,B,C成等差数列且A<B<C,则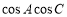 的取值范围是( )
的取值范围是( )
A.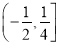 B.
B.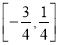 C.
C.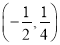 D.
D.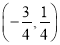
查看答案和解析>>
科目:高中数学 来源:2016届浙江省宁波市高一下学期期末考试数学试卷(解析版) 题型:填空题
已知数列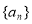 是首项为3,公差为1的等差数列,数列
是首项为3,公差为1的等差数列,数列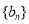 是首项为
是首项为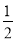 ,公比也为
,公比也为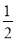 的等比数列,其中
的等比数列,其中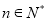 ,那么数列
,那么数列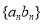 的前
的前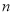 项和
项和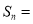 ______.
______.
查看答案和解析>>
科目:高中数学 来源:2016届河南长葛第三实验高中高一下学期第三次考试数学试卷(解析版) 题型:解答题
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60) ...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
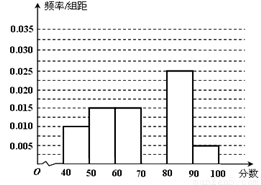
(1)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分;
(3)从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com