
| A. | 数列1,3,4,5可表示为{1,3,4,5} | B. | 数列0,1,2,3,…可表示为{n} | ||
| C. | 数列0,1,0,1,…是常数列 | D. | 数列{$\frac{n}{n+1}$}是递增数列 |
分析 根据数列的概念和数列的函数特征分别判断即可.
解答 解:对于A,数列1,3,4,5可表示为{1,3,4,5},故A错误,
对于B,数列0,1,2,3,…可以表示为{n},n∈N,故B错误,
对于C,数列0,1,0,1,…是摆动数列,故C错误,
对于D,数列{$\frac{n}{n+1}$},$\frac{n}{n+1}$-$\frac{n-1}{n}$=1-$\frac{1}{n+1}$-(1-$\frac{1}{n}$)=$\frac{1}{n}$-$\frac{1}{n+1}$>0,故数列{$\frac{n}{n+1}$}是递增数列,故正确.
故选:D
点评 本题考查了数列的概念和数列的通项公式,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 底面是正方形的四棱柱是正方体 | |
| B. | 棱锥的高线可能在几何体之外 | |
| C. | 有两个面互相平行,其余各面是平行四边形的几何体是棱柱 | |
| D. | 有一个面是多边形,其余各面都是三角形的几何体是棱锥 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 近视 | 不近视 | 总计 | |
| 成绩优秀 | 20 | 16 | 36 |
| 成绩不优秀 | 6 | 18 | 24 |
| 总计 | 26 | 34 | 60 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向量$\overrightarrow{OA}$的长度与向量$\overrightarrow{AO}$的长度相等 | B. | 零向量与任意非零向量平行 | ||
| C. | 长度相等方向相反的向量共线 | D. | 方向相反的向量可能相等 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,-\frac{{\sqrt{3}}}{2})$ | B. | $(-1,-\sqrt{3})$ | C. | $(\frac{1}{2},\frac{{\sqrt{3}}}{2})$ | D. | $(1,\sqrt{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
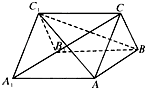 如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2.
如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com