
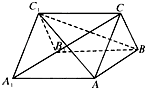
 如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2.
如图,已知ABC-A1B1C1是正三棱柱,它的底面边长和侧棱长都是2.分析 (1)求异面直线所成角,常规思想:平行作角,构造三角形求角;
(2)三棱锥C-ABC1的体积直接求解不太合适,则采用等体积法,可转化为以C1为顶点,以△ABC为底面,再计算体积.
解答 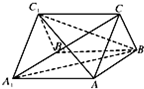 解:(Ⅰ)如图,连接A1B,∵正三棱柱ABC-A1B1C1中,C1B1∥CB,
解:(Ⅰ)如图,连接A1B,∵正三棱柱ABC-A1B1C1中,C1B1∥CB,
∴∠A1CB(或其补角)是异面直线A1C与B1C1所成的角…(2分)
∵四边形AA1C1C与AA1B1B都是边长为2的正方形,
∴$|{{A_1}C}|=|{{A_1}B}|=2\sqrt{2}$,
△A1CB中,根据余弦定理,
得cos∠A1CB=$\frac{2{\sqrt{2}}^{2}+{2}^{2}-2{\sqrt{2}}^{2}}{2×2\sqrt{2}×2}$=$\frac{4}{8\sqrt{2}}=\frac{\sqrt{2}}{4}$…(5分)
∴异面直线A1C与B1C1所成角的余弦值为$\frac{\sqrt{2}}{4}$…(6分)
(Ⅱ)∵△ABC的面积${S_{△ABC}}=\frac{{\sqrt{3}}}{4}×{2^2}=\sqrt{3}$,高CC1=2,
∴正三棱柱ABC-A1B1C1的体积$V={S_{△ABC}}×C{C_1}=2\sqrt{3}$…(8分)
而三棱锥C1-ABC与正三棱柱ABC-A1B1C1同底等高,
∴三棱锥C1-ABC的体积${V_{{C_1}-ABC}}=\frac{1}{3}{V_{ABC-{A_1}{B_1}{C_1}}}=\frac{2}{3}\sqrt{3}$,…(10分)
又∵${V_{C-AB{C_1}}}={V_{{C_1}-ABC}}$,
∴三棱锥C-ABC1的体积为$\frac{2}{3}\sqrt{3}$…(12分)
点评 本题考查了几何体中异面直线所成角的常规求解方法,对三棱锥的体积求解方法:公式法和等体积法;本题所考查的求异面直线所成角的方法和求三棱锥体积的等体积法,均要求学生掌握好,属于中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | 数列1,3,4,5可表示为{1,3,4,5} | B. | 数列0,1,2,3,…可表示为{n} | ||
| C. | 数列0,1,0,1,…是常数列 | D. | 数列{$\frac{n}{n+1}$}是递增数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,5} | B. | [2,4,5} | C. | {2,5,6} | D. | {2,4,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-5=0 | B. | x+y-1=0 | C. | x-y-5=0 | D. | x-y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com