
| x | 2 | 3 | 4 | 5 |
| y | 2.2 | 3.8 | 5.5 | 6.5 |
分析 根据表中数据,求出样本中心点($\overline{x}$,$\overline{y}$),代入回归直线方程即可求出a的值.
解答 解:根据表中数据,得;
$\overline{x}$=$\frac{1}{4}$(2+3+4+5)=$\frac{7}{2}$,
$\overline{y}$=$\frac{1}{4}$(2.2+3.8+5.5+6.5)=$\frac{9}{2}$,
∴回归直线方程$\widehat{y}$=1.46x+a过样本中心($\frac{7}{2}$,$\frac{9}{2}$);
∴实数a=$\frac{9}{2}$-1.46×$\frac{7}{2}$=-0.61.
故答案为:0.61.
点评 本题考查了计算平均数以及利用样本中心点求回归直线方程的应用问题,是基础题目.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
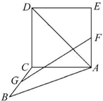 如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
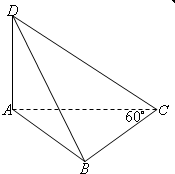 如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )
如图,四面体D-ABC的体积为$\frac{1}{4}$,且满足∠ACB=60°,BC=1,AD+$\frac{AC}{\sqrt{3}}$=2,则四面体D-ABC中最长棱的长度为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
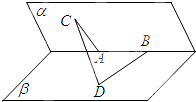 如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.
如图,已知是A,B是直二面角α-l-β的棱上两点,线段AC?α,线段BD?β,且AC⊥l,BD⊥l,AC=AB=6,BD=6$\sqrt{2}$,求线段CD的长.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.28 | B. | 0.44 | C. | 0.56 | D. | 0.84 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com