
(本小题共14分)已知函数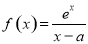 (其中常数
(其中常数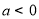 ).
).
(1)求函数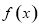 的定义域及单调区间;
的定义域及单调区间;
(2)若存在实数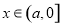 ,使得不等式
,使得不等式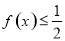 成立,求
成立,求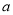 的取值范围.
的取值范围.
(1)定义域为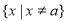 ,单调递增区间为
,单调递增区间为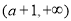 ,单调递减区间为
,单调递减区间为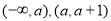 ;
;
(2)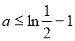 。
。
【解析】
试题分析:(1)由分母不为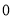 ,可求函数
,可求函数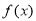 的定义域,对函数
的定义域,对函数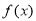 求导,解
求导,解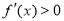 可得
可得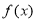 的单调递增区间,解
的单调递增区间,解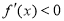 可得
可得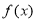 的单调递减区间;(2)若存在实数
的单调递减区间;(2)若存在实数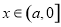 ,使得不等式
,使得不等式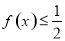 成立,等价于
成立,等价于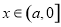 ,
,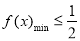 ,通过研究函数
,通过研究函数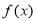 在区间
在区间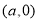 上的单调性可知
上的单调性可知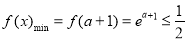 ,可求出
,可求出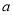 的范围。
的范围。
试题解析:(1)函数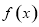 的定义域为
的定义域为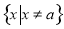 . 1分
. 1分
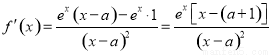 . 3分
. 3分
由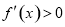 ,解得
,解得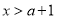 .
.
由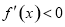 ,解得
,解得 且
且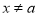 .
.
∴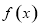 的单调递增区间为
的单调递增区间为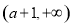 ,单调递减区间为
,单调递减区间为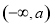 ,
,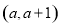 .
.
6分
(2)由题意可知,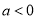 ,且
,且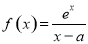 在
在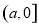 上的最小值小于等于
上的最小值小于等于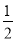 时,存在实数
时,存在实数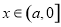 ,使得不等式
,使得不等式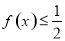 成立. 7分
成立. 7分
若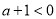 即
即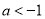 时,
时,
x |
| a+1 |
|
| ? | 0 | + |
| ↘ | 极小值 | ↗ |
∴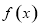 在
在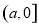 上的最小值为
上的最小值为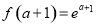 .
.
则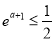 ,得
,得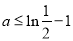 . 10分
. 10分
若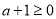 即
即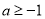 时,
时,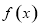 在
在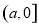 上单调递减,则
上单调递减,则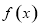 在
在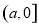 上的最小值为
上的最小值为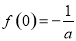 . 11分
. 11分
由 得
得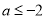 (舍). 132分
(舍). 132分
综上所述,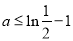 . 14分
. 14分
考点:函数定义域、单调性、函数最值、恒成立问题。


科目:高中数学 来源:2014-2015学年浙江省金华市高三上学期期中考试理科数学试卷(解析版) 题型:填空题
设抛物线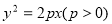 的焦点为F,点A(0,2).若线段FA的中点B在抛物线上,则B到该抛物线准线的距离为________.
的焦点为F,点A(0,2).若线段FA的中点B在抛物线上,则B到该抛物线准线的距离为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com