
分析 (1)基本事件总数n=${A}_{5}^{5}$=120,甲、乙两人的演出序号至少有一个为偶数的对立事件为甲、乙两人的演出序号都是奇数,由此利用对立事件概率计算公式能求出甲、乙两人的演出序号至少有一个为偶数的概率.
(2)甲、乙两人的演出序号不相邻的对立事件是甲、乙两人的演出序号相邻,由此利用对立事件概率计算公式能求出甲、乙两人的演出序号不相邻的概率.
解答 解:(1)在甲、乙等5位学生参加的一次社区专场演唱会中,
每位学生的节目集中安排在一起演出,
采用抽签的方法随机确定各位学生的演出顺序(序号为1,2,3,4,5).
基本事件总数n=${A}_{5}^{5}$=120,
甲、乙两人的演出序号至少有一个为偶数的对立事件为甲、乙两人的演出序号都是奇数,
∴甲、乙两人的演出序号至少有一个为偶数的概率p1=1-$\frac{{A}_{3}^{2}{A}_{3}^{3}}{{A}_{5}^{5}}$=$\frac{7}{10}$.
(2)甲、乙两人的演出序号不相邻的对立事件是甲、乙两人的演出序号相邻,
∴甲、乙两人的演出序号不相邻的概率:
p2=1-$\frac{{A}_{4}^{4}{A}_{2}^{2}}{{A}_{5}^{5}}$=$\frac{3}{5}$.
点评 本题考查概率的求法,以及化简整理的运算能力,属于基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{2}$个周期 | B. | 向右平移$\frac{π}{2}$个周期 | ||
| C. | 向左平移$\frac{π}{4}$个周期 | D. | 向右平移$\frac{π}{4}$个周期 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
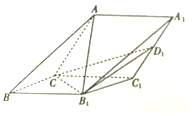 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 明天该地区约有80%的时间会下雨,20%的时间不下雨 | |
| B. | 明天该地区约有80%的地方会下雨,20%的地方不下雨 | |
| C. | 明天该地区下雨的可能性为80% | |
| D. | 该地区约有80%的人认为明天会下雨,20%的人认为明天不下雨 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,2) | C. | $(1\;,\;\;\sqrt{3})$ | D. | $(1\;,\;\;\sqrt{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com