
分析 对于所给的每一个函数,分别计算 $\frac{f{(x}_{1})-f{(x}_{2})}{{{x}_{1}-x}_{2}}$和f′( $\frac{{{x}_{1}+x}_{2}}{2}$)的值,检验二者是否相等,从而根据恒均变函数”的定义,做出判断.
解答 解:对于①f(x)=2x+3,
$\frac{f{(x}_{1})-f{(x}_{2})}{{{x}_{1}-x}_{2}}$=$\frac{{2x}_{1}-{2x}_{2}}{{{x}_{1}-x}_{2}}$=2,f′( $\frac{{{x}_{1}+x}_{2}}{2}$)=2,
满足 $\frac{f{(x}_{1})-f{(x}_{2})}{{{x}_{1}-x}_{2}}$=f′( $\frac{{{x}_{1}+x}_{2}}{2}$),为恒均变函数.
对于②f(x)=$\frac{1}{x}$,
$\frac{f{(x}_{1})-f{(x}_{2})}{{{x}_{1}-x}_{2}}$=$\frac{\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}}}{{{x}_{1}-x}_{2}}$=-$\frac{1}{{{x}_{1}x}_{2}}$,f′( $\frac{{{x}_{1}+x}_{2}}{2}$)=-$\frac{4}{{({{x}_{1}+x}_{2})}^{2}}$,
显然不满足 $\frac{f{(x}_{1})-f{(x}_{2})}{{{x}_{1}-x}_{2}}$=f′( $\frac{{{x}_{1}+x}_{2}}{2}$),故不是恒均变函数.
对于③f(x)=x2-2x+3,
$\frac{f{(x}_{1})-f{(x}_{2})}{{{x}_{1}-x}_{2}}$=$\frac{{(x}_{1}{-x}_{2}){(x}_{1}{+x}_{2}-2)}{{{x}_{1}-x}_{2}}$=x1+x2-2
f′( $\frac{{{x}_{1}+x}_{2}}{2}$)=2•$\frac{{{x}_{1}+x}_{2}}{2}$-2=x1+x2-2,
故满足 $\frac{f{(x}_{1})-f{(x}_{2})}{{{x}_{1}-x}_{2}}$=f′( $\frac{{{x}_{1}+x}_{2}}{2}$)为恒均变函数.
对于④f(x)=ex ,
$\frac{f{(x}_{1})-f{(x}_{2})}{{{x}_{1}-x}_{2}}$=$\frac{{{e}^{{x}_{1}}-e}^{{x}_{2}}}{{{x}_{1}-x}_{2}}$,f′( $\frac{{{x}_{1}+x}_{2}}{2}$)=${e}^{\frac{{{x}_{1}+x}_{2}}{2}}$,
显然不满足$\frac{f{(x}_{1})-f{(x}_{2})}{{{x}_{1}-x}_{2}}$=f′( $\frac{{{x}_{1}+x}_{2}}{2}$),故不是恒均变函数.
对于⑤f(x)=lnx,
$\frac{f{(x}_{1})-f{(x}_{2})}{{{x}_{1}-x}_{2}}$=$\frac{l{nx}_{1}-l{nx}_{2}}{{{x}_{1}-x}_{2}}$=$\frac{ln\frac{{x}_{1}}{{x}_{2}}}{{{x}_{1}-x}_{2}}$,f′( $\frac{{{x}_{1}+x}_{2}}{2}$)=$\frac{2}{{{x}_{1}+x}_{2}}$,
显然不满足 $\frac{f{(x}_{1})-f{(x}_{2})}{{{x}_{1}-x}_{2}}$=f′( $\frac{{{x}_{1}+x}_{2}}{2}$),故不是恒均变函数.
故答案为:①③.
点评 本题主要考查函数的导数运算,“恒均变函数”的定义,判断命题的真假.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{41}{26}$ | B. | $\frac{23}{14}$ | C. | $\frac{11}{7}$ | D. | $\frac{11}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
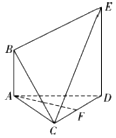 如图所示的多面体ABCDE中,已知AB∥DE,AB⊥AD,AD=2$\sqrt{3}$,AC=CD=DE=2AB=2,BC=$\sqrt{5}$,F是CD的中点.
如图所示的多面体ABCDE中,已知AB∥DE,AB⊥AD,AD=2$\sqrt{3}$,AC=CD=DE=2AB=2,BC=$\sqrt{5}$,F是CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com