
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() ,且平面
,且平面![]() 平面
平面![]() .
.

(1)求证: ![]() ;
;
(2)若![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】【试题分析】(1)连接![]() ,根据菱形的几何性质有
,根据菱形的几何性质有![]() ,由面面垂直的性质定理可知
,由面面垂直的性质定理可知![]() 平面
平面![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() .(2) 设
.(2) 设![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,以
,以![]() 为坐标原点建立空间直角坐标系,通过计算平面
为坐标原点建立空间直角坐标系,通过计算平面![]() 和平面
和平面![]() 的法向量来求二面角的余弦值.
的法向量来求二面角的余弦值.
【试题解析】
(1)证明:
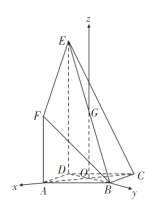
连接![]() ,由四边形
,由四边形![]() 为菱形可知
为菱形可知![]() ,
,
∵平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ;
;
(2)解:设![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,
,
由(1)可知![]() 两两互相垂直,
两两互相垂直,
则可建立如图所示的空间直角坐标系![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ,即
,即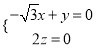 ,
,
取![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
同理可得![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
则![]() ,
,
又二面角![]() 的平面角为钝角,则其余弦值为
的平面角为钝角,则其余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点A(0,-2),椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为![]() ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的动直线l与E相交于P,Q两点.当△OPQ的面积最大时,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该公司将最近承揽的
元.该公司将最近承揽的![]() 件包裹的重量统计如下:
件包裹的重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近![]() 天,每天揽件数量统计如下表:
天,每天揽件数量统计如下表:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来![]() 天内恰有
天内恰有![]() 天揽件数在
天揽件数在![]() 之间的概率;
之间的概率;
(2)(i)估计该公司对每件包裹收取的快递费的平均值;
(ii)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,工资
件,工资![]() 元.公司正在考虑是否将前台工作人员裁减
元.公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三角形的面积为![]() ,其中
,其中![]() ,
,![]() ,
,![]() 为三角形的边长,
为三角形的边长,![]() 为三角形内切圆的半径,则利用类比推理,可得出四面体的体积为( )
为三角形内切圆的半径,则利用类比推理,可得出四面体的体积为( )
A. ![]()
B. ![]()
C. ![]() ,(
,(![]() 为四面体的高)
为四面体的高)
D. ![]() ,(
,(![]() ,
,![]() ,
,![]() ,
,![]() 分别为四面体的四个面的面积,
分别为四面体的四个面的面积,![]() 为四面体内切球的半径)
为四面体内切球的半径)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为![]() ,则称该数为“完美四位数”,如数字“
,则称该数为“完美四位数”,如数字“![]() ”.试问用数字
”.试问用数字![]() 组成的无重复数字且大于
组成的无重复数字且大于![]() 的“完美四位数”有( )个
的“完美四位数”有( )个
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com