
【题目】如图,已知多面体![]() 的底面
的底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,
, ![]() ,且
,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
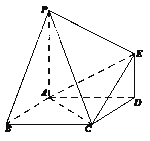
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析: (1)连接BD,交AC于点O,设PC中点为F,由已知结合三角形中位线定理可得四边形OFED为平行四边形,则OD∥EF,即BD∥EF.再由PA⊥平面ABCD,可得PA⊥BD.又ABCD是菱形,得BD⊥AC.由线面垂直的判定可得BD⊥平面PAC.则EF⊥平面PAC.进一步得到平面PAC⊥平面PCE.
(2)由∠ABC=60°,可得△ABC是等边三角形,得AC=2.再由PA⊥平面ABCD,得PA⊥AC.求出三角形PAC的面积证得EF是三棱锥E﹣PAC的高,利用P﹣ACE的体积等于E﹣PAC的体积求解.
解析:
(1)证明:连接![]() ,交
,交![]() 于点
于点![]() ,设
,设![]() 中点为
中点为![]() ,
,
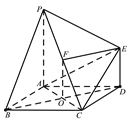 连接
连接 ![]() ,
, ![]() .
.
因为![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,
所以![]() ,且
,且![]() ,
,
因为![]() ,且
,且![]() ,
,
所以![]() ,且
,且![]()
所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,即
,即![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() 是菱形,所以
是菱形,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面 ![]()
因为![]() ,所以
,所以![]()
![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]()
(2)因为![]() ,所以△
,所以△![]() 是等边三角形,所以
是等边三角形,所以![]() .
.
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,![]()
![]() .
.![]()
因为![]() 面
面![]() ,所以
,所以![]() 是三棱锥
是三棱锥![]() 的高,
的高,![]()
![]() ,
,![]()
![]()
![]() 平面
平面![]() ,
,![]()
![]()
所以点![]() 到平面
到平面![]() 的距离
的距离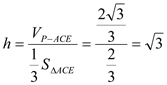


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】以下对各事件发生的概率判断正确的是( )
A.甲、乙两人玩剪刀、石头、布的游戏,则玩一局甲不输的概率是![]()
B.从1名男同学和2名女同学中任选2人参加社区服务,则选中一男一女同学的概率为![]()
C.将一个质地均匀的正方体骰子(每个面上分别写有数字1,2,3,4,5,6)先后抛掷2次,观察向上的点数,则点数之和是6的概率是![]()
D.从三件正品、一件次品中随机取出两件,则取出的产品全是正品的概率是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论:
①若![]() ,则“
,则“![]() ”成立的一个充分不必要条件是“
”成立的一个充分不必要条件是“![]() ,且
,且![]() ”;
”;
②存在![]() ,使得
,使得![]() ;
;
③若函数![]() 的导函数是奇函数,则实数
的导函数是奇函数,则实数![]() ;
;
④平面上的动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到
到![]() 轴的距离大1的点
轴的距离大1的点![]() 的轨迹方程为
的轨迹方程为![]() .
.
其中正确结论的序号为_________.(填写所有正确的结论序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y(万元)的几组对照数据:
x(年) | 2 | 3 | 4 | 5 | 6 |
y(万元) | 1 | 2.5 | 3 | 4 | 4.5 |
(1)若知道y对x呈线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?参考公式: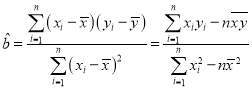 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高二年级组织外出参加学业水平考试,出行方式为:乘坐学校定制公交或自行打车前往,大数据分析显示,当![]() 的学生选择自行打车,自行打车的平均时间为
的学生选择自行打车,自行打车的平均时间为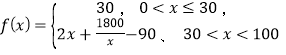 (单位:分钟) ,而乘坐定制公交的平均时间不受
(单位:分钟) ,而乘坐定制公交的平均时间不受![]() 影响,恒为40分钟,试根据上述分析结果回答下列问题:
影响,恒为40分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
在什么范围内时,乘坐定制公交的平均时间少于自行打车的平均时间?
(2)求该校学生参加考试平均时间![]() 的表达式:讨论
的表达式:讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
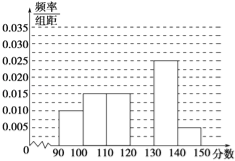
(1)求分数在[120,130)内的频率;
(2)若在同一组数据中,将该组区间的中点值(如:组区间[100,110)的中点值为![]() =105)作为这组数据的平均分,据此,估计本次考试的平均分;
=105)作为这组数据的平均分,据此,估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具所需成本费用为P元,且P=1 000+5x+![]() x2,而每套售出的价格为Q元,其中Q(x)=a+
x2,而每套售出的价格为Q元,其中Q(x)=a+![]() (a,b∈R),
(a,b∈R),
(1)问:玩具厂生产多少套时,使得每套所需成本费用最少?
(2)若生产出的玩具能全部售出,且当产量为150套时利润最大,此时每套价格为30元,求a,b的值.(利润=销售收入-成本).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com