
����Ŀ��ijУ�ӲμӸ���ģ�⿼�Ե�ѧ���������ȡ60��ѧ����������ѧ�ɼ�����Ϊ�������ֳ�����[90��100����[100��110��������[140��150]��õ����²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�ε���Ϣ���ش��������⣺
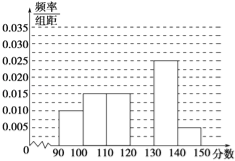
��1���������[120��130���ڵ�Ƶ�ʣ�
��2������ͬһ�������У�������������е�ֵ���磺������[100��110�����е�ֵΪ![]() =105����Ϊ�������ݵ�ƽ���֣��ݴˣ����Ʊ��ο��Ե�ƽ���֣�
=105����Ϊ�������ݵ�ƽ���֣��ݴˣ����Ʊ��ο��Ե�ƽ���֣�
��3���÷ֲ�����ķ����ڷ�����Ϊ[110��130����ѧ���г�ȡһ������Ϊ6��������������������һ�����壬������ȡ2�ˣ���������1���ڷ�����[120��130���ڵĸ��ʣ�
���𰸡�������0.3; ������121;������![]() .
.
����������1��������[120��130���ڵ�Ƶ��Ϊ
1����0.1+0.15+0.15+0.25+0.05��=1��0.7=0.3��
��2������ƽ����Ϊ
![]() =95��0.1+105��0.15+115��0.15+125��0.3+135��0.25+145��0.05=121��
=95��0.1+105��0.15+115��0.15+125��0.3+135��0.25+145��0.05=121��
��3�������⣬[110��120�������ε�����Ϊ60��0.15=9���ˣ���
[120��130�������ε�����Ϊ60��0.3=18���ˣ���
���÷ֲ�����ķ����ڷ�����Ϊ[110��130����ѧ���г�ȡһ������Ϊ6��������
������[110��120���������ڳ�ȡ2�ˣ����ֱ��Ϊm��n��
��[120��130���������ڳ�ȡ4�ˣ����ֱ��Ϊa��b��c��d��
��������������ȡ2�ˣ�������1���ڷ�����[120��130������Ϊ�¼�A��
������¼��У�m��n������m��a����������m��d������n��a����������n��d������a��b����������c��d����15�֣�
���¼�A�����Ļ����¼��У�m��n������m��a������m��b������m��c������m��d������n��a������n��b������n��c������n��d����9�֣�
��P��A��=![]() =
=![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��x��[0��1]ʱ������y=��mx��1��2 ��ͼ����y= ![]() +m��ͼ������ֻ��һ�����㣬����ʵ��m��ȡֵ��Χ�ǣ�������
+m��ͼ������ֻ��һ�����㣬����ʵ��m��ȡֵ��Χ�ǣ�������
A.��0��1]��[2 ![]() ��+�ޣ�
��+�ޣ�
B.��0��1]��[3��+�ޣ�
C.��0�� ![]() ����[2
����[2 ![]() ��+�ޣ�
��+�ޣ�
D.��0�� ![]() ]��[3��+�ޣ�
]��[3��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼��ij�������һ�������ߵ��������̣�����Աÿ��30 min�Ӹ��������������ȡһ���������������ߴ�(��λ��cm)�������Ǽ���Ա��һ�������γ�ȡ��16������ijߴ磺
��ȡ˳�� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
����ߴ� | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
��ȡ���� | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
����ߴ� | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
�������![]() =
=![]() xi=9.97��s=
xi=9.97��s=![]() =
=![]() ��0.212��
��0.212��![]() ��18.439��
��18.439��![]() ��xi��
��xi��![]() ����i��8.5��=��2.78��
����i��8.5��=��2.78��
������xiΪ��ȡ�ĵ�i������ijߴ磬i��1��2������16.
��(1)��(xi��i)(i��1��2������16)�����ϵ��r�����ش��Ƿ������Ϊ��һ������������ߴ粻������
�����̵Ľ��ж�ϵͳ�ر����С(��|r|��0.25���������Ϊ����ijߴ粻���������̵Ľ��ж�ϵͳ��
�������С)��
��(2)һ���ڳ������У���������˳ߴ�����![]() ��3s��
��3s��![]() +3s��֮������������Ϊ��������������һ��
+3s��֮������������Ϊ��������������һ��
�����������̿��ܳ������쳣�������Ե�����������̽��м�飮
���ٴ���һ����Ľ�������Ƿ���Ե�����������̽��м�飿
��������![]() ��3s��
��3s��![]() +3s��֮������ݳ�Ϊ��Ⱥֵ��������Ⱥֵ���������������ߵ�������������ߴ��
+3s��֮������ݳ�Ϊ��Ⱥֵ��������Ⱥֵ���������������ߵ�������������ߴ��
����ֵ����(��ȷ��0.01)
����������xi��yi����i=1��2������n�������ϵ��r=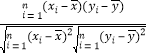 ��
��![]() ��0.09��
��0.09��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���賣��![]() ������
������![]() .
.
(1) ��![]() ����
����![]() �ĵ����ݼ����䣻
�ĵ����ݼ����䣻
(2) ��![]() Ϊ�溯�����ҹ���
Ϊ�溯�����ҹ���![]() �IJ���ʽ
�IJ���ʽ![]() �����е�
�����е�![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(3) ��![]() ʱ��������
ʱ��������![]() ����������ȵ�ʵ����
����������ȵ�ʵ����![]() ��
��![]() ��
��![]() ����
����![]() ����ʵ��
����ʵ��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ζ�ȫ��50��ѧ����ѧϰ�����ԺͶԴ��༶������̬�Ƚ����˵��飬ͳ���������±���ʾ��
���� | �����μ� �༶���� | ��̫������ �Ӱ༶���� | �ܼ� |
ѧϰ�����Ը� | 18 | 7 | 25 |
ѧϰ������һ�� | 6 | 19 | 25 |
�ܼ� | 24 | 26 | 50 |
(1)���������������һ��ѧ������ô�鵽�����μӰ༶������ѧ���ĸ����Ƕ��٣��鵽��̫�����μӰ༶������ѧϰ������һ���ѧ���ĸ����Ƕ��٣�
(2)�����ö����Լ����˼�뷽��������ѧ����ѧϰ��������Դ��༶������̬���Ƿ��йأ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͳ�ƾ־�ij�ؾ���������������![]() �ˣ��������������ݻ���������Ƶ�ʷ�
�ˣ��������������ݻ���������Ƶ�ʷ�
��ֱ��ͼ��ÿ�����������˵㣬�������Ҷ˵㣬���һ���ʾ������![]() ����
����

��1���������������![]() ��Ƶ�ʣ�
��Ƶ�ʣ�
��2������Ƶ�ʷֲ�ֱ��ͼ����������ݵ���λ����
��3��Ϊ�˷�����������������䡢ְҵ�ȷ���Ĺ�ϵ�����밴�������ٴ���![]() ���зֲ�����������
���зֲ�����������![]() ������һ������������������
������һ������������������![]() �����Ӧ������ˣ�
�����Ӧ������ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}���㣺a1=1��nan+1����n+1��an=1��n��N+��
��1��������{an}��ͨ�ʽ��
��2���� ![]() ��������{bn}������
��������{bn}������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��x��R��
��x��R��
��1��֤����a��b��R����a��b�����У�|f��a����f��b��|��|a��b|��
��2����a��b��c��R���� ![]() ��֤����a+b+c��ab+bc+ca��
��֤����a+b+c��ab+bc+ca��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)��ax2��bln x��x��1���м�ֵ![]() .
.
(1)��a��b��ֵ��
(2)����y��f(x)�ĵ����ԣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com