
【题目】已知数列{an}满足:a1=1,nan+1﹣(n+1)an=1(n∈N+)
(1)求数列{an}的通项公式;
(2)若 ![]() ,求数列{bn}的最大项.
,求数列{bn}的最大项.
【答案】
(1)解:已知式可化为 ![]() .
.
则当n≥2时, ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
…
![]() ﹣
﹣ ![]() =1﹣
=1﹣ ![]() ,
,
以上各式相加: ![]() ﹣
﹣ ![]() =1﹣
=1﹣ ![]() ,
,
整理得:an=2n﹣1,
当n=1时,显然成立,
∴数列{an}的通项公式an=2n﹣1;(n∈N+)
(2)解:由 ![]() ,则bn=n×(
,则bn=n×( ![]() )n,n∈N+,
)n,n∈N+,
设g(x)=x( ![]() )x,x>0,求导g′(x)=(
)x,x>0,求导g′(x)=( ![]() )x+x(
)x+x( ![]() )xln(
)xln( ![]() ),
),
令g′(x)=0,解得:x=﹣ ![]() ,8<﹣
,8<﹣ ![]() <9,
<9,
由g(x)在(0,﹣ ![]() )单调递增,在(﹣
)单调递增,在(﹣ ![]() ,+∞)单调递减,
,+∞)单调递减,
且 ![]() ,
,
∴数列{bn}的单调性得最大项为 ![]()
【解析】(1)由 ![]() .采用累加法即可求得数列{an}的通项公式;(2)由(1)可知bn=n×(
.采用累加法即可求得数列{an}的通项公式;(2)由(1)可知bn=n×( ![]() )n , n∈N+ , 根据导数与函数单调性的关系,即可求得数列{bn}的最大项.
)n , n∈N+ , 根据导数与函数单调性的关系,即可求得数列{bn}的最大项.
【考点精析】掌握数列的通项公式是解答本题的根本,需要知道如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={a1 , a2 , …,am}.若集合A1∪A2∪A3∪…∪An=A,则称A1 , A2 , A3 , …,An为集合A的一种拆分,所有拆分的个数记为f(n,m).
(1)求f(2,1),f(2,2),f(3,2)的值;
(2)求f(n,2)(n≥2,n∈N*)关于n的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图形的信息,回答下列问题:
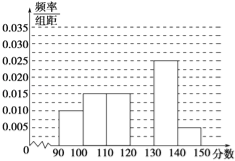
(1)求分数在[120,130)内的频率;
(2)若在同一组数据中,将该组区间的中点值(如:组区间[100,110)的中点值为![]() =105)作为这组数据的平均分,据此,估计本次考试的平均分;
=105)作为这组数据的平均分,据此,估计本次考试的平均分;
(3)用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2人,求至多有1人在分数段[120,130)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》中的更相减损法的思路与图相似.执行该程序框图,若输入的a,b分别为14,18,则输出的a=( ) 
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据:

(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测技改后生产100吨甲产品比技改前少消耗多少吨标准煤.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x(ex﹣1)﹣ax2(e=2.71828…是自然对数的底数).
(1)若 ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)若f(x)在(﹣1,0)内无极值,求a的取值范围;
(3)设n∈N* , x>0,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点P(![]() ,1),直线l的参数方程为
,1),直线l的参数方程为 (t为参数)若以O为极点,以Ox为极轴,选择相同的单位长度建立极坐标系,则曲线C的极坐标方程为ρ=
(t为参数)若以O为极点,以Ox为极轴,选择相同的单位长度建立极坐标系,则曲线C的极坐标方程为ρ=![]() cos(θ-
cos(θ-![]() )
)
(Ⅰ)求直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)设直线l与曲线C相交于A,B两点,求点P到A,B两点的距离之积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com