
【题目】设函数f(x)=x(ex﹣1)﹣ax2(e=2.71828…是自然对数的底数).
(1)若 ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)若f(x)在(﹣1,0)内无极值,求a的取值范围;
(3)设n∈N* , x>0,求证: ![]() .
.
【答案】
(1)解:当 ![]() 时,
时, ![]()
所以f'(x)=ex﹣1+xex﹣x=(ex﹣1)(x+1)
当x∈(﹣∞,﹣1)时,f'(x)>0;当x∈(﹣1,0)时,f'(x)<0;
当x∈(0,+∞)时,f'(x)>0
故f(x)在(﹣∞,﹣1),(0,+∞)单调递增,在(﹣1,0)单调递减
(2)解:若f(x)在(﹣1,0)内无极值,则f(x)在(﹣1,0)上单调,
又f'(x)=(x+1)ex﹣2ax﹣1
①若f(x)在(﹣1,0)上递减,则f'(x)≤0,对x∈(﹣1,0)恒成立,
于是有 ![]() ,令
,令 ![]() ,
,
下面证明h(x)在(﹣∞,0)上单调递增: ![]() ,令r(x)=(r﹣1)ex+1,则r'(x)=(x﹣1)ex+ex=xex
,令r(x)=(r﹣1)ex+1,则r'(x)=(x﹣1)ex+ex=xex
当x<0时,r'(x)<0,r(x)单调递减,r(x)>r(0)=0,h'(x)>0h(x)在(﹣∞,0)单调递增.
当x∈(﹣1,0)时,由g(x)=ex+h(x)是增函数,得g(x)>g(﹣1)=1.
由2a≤g(x),得 ![]() ;
;
②若f(x)在(﹣1,0)上单调递增,则f'(x)≥0,对x∈(﹣1,0)恒成立,
于是2a≥g(x),当x∈(﹣1,0)时,由ex>x+1得 ![]() ,
,
从而增函数g(x)=ex+h(x)<2,这样2a>2,a>1.综上得 ![]()
(3)证明:用数学归纳法证明①当n=1时,ex>x+1,不等式成立;
②假设n=k时不等式成立,即 ![]() ,
,
当n=k+1时,令 ![]()
显然(0)=0,由归纳假设, ![]() 对x>0成立,
对x>0成立,
所以(x)在(0,+∞)上单调递增,当x>0时,(x)>(0)=0,即当n=k+1
时,不等式也成立.
综合①②n∈N+,x>0时, ![]()
【解析】(1)当 ![]() 时,f'(x)=ex﹣1+xex﹣x=(ex﹣1)(x+1),由此利用导数性质能求出函数f(x)的单调区间.(2)若f(x)在(﹣1,0)内无极值,则f(x)在(﹣1,0)上单调,又f'(x)=(x+1)ex﹣2ax﹣1,由此利用分类讨论思想及导数的性质能求出a的取值范围.(3)用数学归纳法能证明
时,f'(x)=ex﹣1+xex﹣x=(ex﹣1)(x+1),由此利用导数性质能求出函数f(x)的单调区间.(2)若f(x)在(﹣1,0)内无极值,则f(x)在(﹣1,0)上单调,又f'(x)=(x+1)ex﹣2ax﹣1,由此利用分类讨论思想及导数的性质能求出a的取值范围.(3)用数学归纳法能证明 ![]() .
.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:
【题目】第二届世界青年奥林匹克运动会,中国获37金,13银,13铜共63枚奖牌居奖牌榜首位,并打破十项青奥会记录.由此许多人认为中国进入了世界体育强国之列,也有许多人持反对意见.有网友为此进行了调查,在参加调查的2 548名男性公民中有1 560名持反对意见,2 452名女性公民中有1 200人持反对意见,在运用这些数据说明中国的奖牌数是否与中国进入体育强国有无关系时,用什么方法最有说服力( )
A. 平均数与方差 B. 回归直线方程
C. 独立性检验 D. 概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
分类 | 积极参加 班级工作 | 不太主动参 加班级工作 | 总计 |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
总计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=1,nan+1﹣(n+1)an=1(n∈N+)
(1)求数列{an}的通项公式;
(2)若 ![]() ,求数列{bn}的最大项.
,求数列{bn}的最大项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
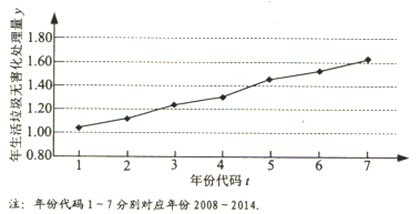
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
参考公式:相关系数
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,x∈R.
,x∈R.
(1)证明对a、b∈R,且a≠b,总有:|f(a)﹣f(b)|<|a﹣b|;
(2)设a、b、c∈R,且 ![]() ,证明:a+b+c≥ab+bc+ca.
,证明:a+b+c≥ab+bc+ca.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足f(x+2)=2f(x),且当x∈[2,4]时, 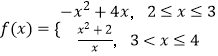 ,g(x)=ax+1,对x1∈[﹣2,0],x2∈[﹣2,1],使得g(x2)=f(x1),则实数a的取值范围为( )
,g(x)=ax+1,对x1∈[﹣2,0],x2∈[﹣2,1],使得g(x2)=f(x1),则实数a的取值范围为( )
A.![]()
B.![]()
C.(0,8]
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查某医院某段时间内婴儿出生的时间与性别的关系,得到下面的数据:出生时间在晚上的男婴为24人,女婴为8人;出生时间在白天的男婴为31人,女婴为26人.
(1)将2×2列联表补充完整.
性别 | 出生时间 | 总计 | |
晚上 | 白天 | ||
男婴 | |||
女婴 | |||
总计 | |||
(2)能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com