Question

【题目】已知定义在R上的函数f（x）满足f（x+2）=2f（x），且当x∈[2，4]时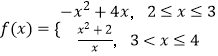， ，g（x）=ax+1，对x1∈[﹣2，0]，x2∈[﹣2，1]，使得g（x2）=f（x1），则实数a的取值范围为（ ）
A.
B.
C.（0，8]
D.

Answer 1

【答案】D
【解析】解：∵f（x）在[2，3]上单调递减，在（3，4]上单调递增， ∴f（x）在[2，3]上的值域为[3，4]，在（3，4]上的值域为（ ， ]，
∴f（x）在[2，4]上的值域为[3， ]，
∵f（x+2）=2f（x），
∴f（x）= f（x+2）= f（x+4），
∴f（x）在[﹣2，0]上的值域为[ ， ]，
当a＞0时，g（x）为增函数，g（x）在[﹣2，1]上的值域为[﹣2a+1，a+1]，
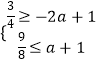∴ ，解得a≥ ；
当a＜0时，g（x）为减函数，g（x）在[﹣2，1]上的值域为[a+1，﹣2a+1]，
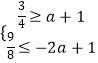∴ ，解得a≤﹣ ；
当a=0时，g（x）为常数函数，值域为{1}，不符合题意；
综上，a的范围是a≥ 或a≤﹣ ．
故选：D．