练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知，则方程实数根的个数为 （ ）

    A. 7 B. 6 C. 5 D. 4

    【答案】A

    【解析】

    由方程f[f（x）]=2先求出f（x）=1或f（x）=或f（x）=5，再解方程即可．

    ①当f（x）≤1时，

    f[f（x）]==2，

    解得，f（x）=1，

    ∴=1或|log2（x﹣1）|=1，

    ∴x﹣1=或x﹣1=2，

    故x=或x=3；

    ②若f（x）＞1，则f[f（x）]=|log2（f（x）﹣1）|=2，

    ∴f（x）﹣1=或f（x）﹣1=4，

    ∴f（x）=或f（x）=5，

    若f（x）=，则=或|log2（x﹣1）|=，

    则x=﹣1或x=1+或x=1+；

    若f（x）=5，则=5或|log2（x﹣1）|=5，

    则x=3（舍去）或x=1+2﹣5或x=1+25，

    综上所述，方程f[f（x）]=2实数根的个数是7，

    故答案为：A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）是定义在R上的偶函数，当x≥0时，f（x）=x2﹣2x﹣1．
    （1）求f（x）的函数解析式，并用分段函数的形式给出；
    （2）作出函数f（x）的简图；
    （3）写出函数f（x）的单调区间及最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：

    零件的个数（个）

    2

    3

    4

    5

    加工的时间（小时）

    2.5

    3

    4

    4.5

    （Ⅰ）在给定的坐标系中画出表中数据的散点图；

    （Ⅱ）试对与的关系进行相关性检验,如与具有线性相关关系,求出对的回归直线方程；

    （Ⅲ）试预测加工个零件需要多少时间？

    参考数据：，.

    附：)；, ；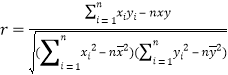

    相关性检验的临界值表

    n-2

    小概率

    n-2

    小概率

    n-2

    小概率

    0.05

    0.01

    0.05

    0.01

    0.05

    0.01

    1

    0.997

    1

    4

    0.811

    0.917

    7

    0.666

    0.798

    2

    0.950

    0.990

    5

    0.754

    0.874

    8

    0.632

    0.765

    3

    0.878

    0.959

    6

    0.707

    0.834

    9

    0.602

    0.735

    注：表中的n为数据的组数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知当x∈[0，1]时，函数y=（mx﹣1）2 的图象与y= +m的图象有且只有一个交点，则正实数m的取值范围是（　　）
    A.（0，1]∪[2 ，+∞）
    B.（0，1]∪[3，+∞）
    C.（0， ）∪[2 ，+∞）
    D.（0， ]∪[3，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=sin（ωx﹣ ）+sin（ωx﹣ ），其中0＜ω＜3，已知f（ ）=0．（12分）
    （Ⅰ）求ω；
    （Ⅱ）将函数y=f（x）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移 个单位，得到函数y=g（x）的图象，求g（x）在[﹣ ， ]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 ， 的夹角为120°，且| |=2，| |=3，则向量2 +3 在向量2 + 方向上的投影为（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第二届世界青年奥林匹克运动会，中国获37金，13银，13铜共63枚奖牌居奖牌榜首位，并打破十项青奥会记录．由此许多人认为中国进入了世界体育强国之列，也有许多人持反对意见．有网友为此进行了调查，在参加调查的2 548名男性公民中有1 560名持反对意见，2 452名女性公民中有1 200人持反对意见，在运用这些数据说明中国的奖牌数是否与中国进入体育强国有无关系时，用什么方法最有说服力(　　)

    A. 平均数与方差 B. 回归直线方程

    C. 独立性检验 D. 概率

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了监控某种零件的一条生产线的生产过程，检验员每隔30 min从该生产线上随机抽取一个零件，并测量其尺寸(单位：cm)．下面是检验员在一天内依次抽取的16个零件的尺寸：

    抽取顺序

    1

    2

    3

    4

    5

    6

    7

    8

    零件尺寸

    9.95

    10.12

    9.96

    9.96

    10.01

    9.92

    9.98

    10.04

    抽取次序

    9

    10

    11

    12

    13

    14

    15

    16

    零件尺寸

    10.26

    9.91

    10.13

    10.02

    9.22

    10.04

    10.05

    9.95

    经计算得=xi=9.97，s==≈0.212，≈18.439，（xi﹣）（i﹣8.5）=﹣2.78，

    　其中xi为抽取的第i个零件的尺寸，i＝1，2，…，16.

    　(1)求(xi，i)(i＝1，2，…，16)的相关系数r，并回答是否可以认为这一天生产的零件尺寸不随生产

    　过程的进行而系统地变大或变小(若|r|＜0.25，则可以认为零件的尺寸不随生产过程的进行而系统地

    　变大或变小)．

    　(2)一天内抽检零件中，如果出现了尺寸在（﹣3s，+3s）之外的零件，就认为这条生产线在这一天

    　的生产过程可能出现了异常情况，需对当天的生产过程进行检查．

    　①从这一天抽检的结果看，是否需对当天的生产过程进行检查？

    　②在（﹣3s，+3s）之外的数据称为离群值，试剔除离群值，估计这条生产线当天生产的零件尺寸的

    　均值与标准差．(精确到0.01)

    附：样本（xi，yi）（i=1，2，…，n）的相关系数r=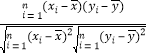，≈0.09．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足：a1=1，nan+1﹣（n+1）an=1（n∈N+）
    （1）求数列{an}的通项公式；
    （2）若 ，求数列{bn}的最大项．

    查看答案和解析>>

    同步练习册答案