
【题目】已知F为抛物线![]() 焦点,A为抛物线C上的一动点,抛物线C在A处的切线交y轴于点B,以FA、FB为邻边作平行四边形FAMB.
焦点,A为抛物线C上的一动点,抛物线C在A处的切线交y轴于点B,以FA、FB为邻边作平行四边形FAMB.
(1)证明:点M在一条定直线上;
(2)记点M所在定直线为l,与y轴交于点N,MF与抛物线C交于P,Q两点,求![]() 的面积的取值范围.
的面积的取值范围.
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的焦点为
的焦点为![]() ,
,![]() (其中
(其中![]() )是
)是![]() 上的一点,且
上的一点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)已知![]() 为抛物线
为抛物线![]() 上除顶点
上除顶点![]() 之外的任意一点,在点
之外的任意一点,在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,过
,过![]() 点的直线
点的直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,设
两点,设![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从中国教育在线官方公布的考研动机调查来看,本科生扎堆考研的原因大概集中在这6个方面:本科就业压力大,提升竞争力;通过考研选择真正感兴趣的专业;为了获得学历;继续深造;随大流;有名校情结.如图是2015~2019年全国硕士研究生报考人数趋势图(单位:万人)的折线图.

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,预测2021年全国硕士研究生报考人数.
参考数据:![]() .
.
回归方程![]() 中斜率和截距的最小二乘估计公式分别:
中斜率和截距的最小二乘估计公式分别: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,若曲线
,若曲线![]() 与曲线
与曲线![]() 关于直线
关于直线![]() 对称.
对称.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为
的异于极点的交点为![]() ,与
,与![]() 的异于极点的交点为
的异于极点的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有种特产水果很受当地老百姓欢迎,但该种水果只能在9月份销售,且该种水果只能当天食用口感最好,隔天食用口感较差。某超市每年9月份都销售该特产水果,每天计划进货量相同,进货成本每公斤8元,销售价每公斤12元;当天未卖出的水果则转卖给水果罐头厂,但每公斤只能卖到5元。根据往年销售经验,每天需求量与当地气温范围有一定关系。如果气温不低于30度,需求量为5000公斤;如果气温位于![]() ,需求量为3500公斤;如果气温低于25度,需求量为2000公斤;为了制定今年9月份订购计划,统计了前三年9月份的气温范围数据,得下面的频数分布表
,需求量为3500公斤;如果气温低于25度,需求量为2000公斤;为了制定今年9月份订购计划,统计了前三年9月份的气温范围数据,得下面的频数分布表
气温范围 |
|
|
|
|
|
天数 | 4 | 14 | 36 | 21 | 15 |
以气温范围位于各区间的频率代替气温范围位于该区间的概率.
(1)求今年9月份这种水果一天需求量![]() (单位:公斤)的分布列和数学期望;
(单位:公斤)的分布列和数学期望;
(2)设9月份一天销售特产水果的利润为![]() (单位:元),当9月份这种水果一天的进货量为
(单位:元),当9月份这种水果一天的进货量为![]() (单位:公斤)为多少时,
(单位:公斤)为多少时,![]() 的数学期望达到最大值,最大值为多少?
的数学期望达到最大值,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 是椭圆上一点,
是椭圆上一点,![]() 是
是![]() 和
和![]() 的等差中项.
的等差中项.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若![]() 为椭圆的右顶点,直线
为椭圆的右顶点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的另一直线与椭圆交于
的另一直线与椭圆交于![]() 、
、![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某国营企业集团公司现有员工1000名,平均每人每年创造利润10万元.为了激化内部活力,增强企业竞争力,集团公司董事会决定优化产业结构,调整出![]() (
(![]() )名员工从事第三产业;调整后,他们平均每人每年创造利润
)名员工从事第三产业;调整后,他们平均每人每年创造利润![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() %.
%.
(Ⅰ)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(Ⅱ)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则实数![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,A1B1⊥A1C1,D是B1C1的中点,A1A=A1B1=2.

(1)求证:AB1∥平面A1CD;
(2)若异面直线AB1和BC所成角为60°,求四棱锥A1﹣CDB1B的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() 平面PCD,
平面PCD,![]() ,
,![]() ,
,![]() ,E为AD的中点,AC与BE相交于点O.
,E为AD的中点,AC与BE相交于点O.
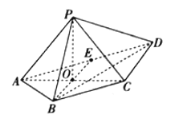
(1)证明:![]() 平面ABCD.
平面ABCD.
(2)求直线BC与平面PBD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com