
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,点
,点![]() 是椭圆上一点,
是椭圆上一点,![]() 是
是![]() 和
和![]() 的等差中项.
的等差中项.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若![]() 为椭圆的右顶点,直线
为椭圆的右顶点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 的另一直线与椭圆交于
的另一直线与椭圆交于![]() 、
、![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
科目:高中数学 来源: 题型:
【题目】![]() 企业为了监控某种零件的一条流水生产线的产品质量,检验员从该生产线上随机抽取100个零件,测量其尺寸
企业为了监控某种零件的一条流水生产线的产品质量,检验员从该生产线上随机抽取100个零件,测量其尺寸![]() (单位:
(单位:![]() )并经过统计分析,得到这100个零件的平均尺寸为10,标准差为0.5.企业规定:若
)并经过统计分析,得到这100个零件的平均尺寸为10,标准差为0.5.企业规定:若![]() ,该零件为一等品,企业获利20元;若
,该零件为一等品,企业获利20元;若![]() 且
且![]() ,该零件为二等品,企业获利10元;否则,该零件为不合格品,企业损失40元.
,该零件为二等品,企业获利10元;否则,该零件为不合格品,企业损失40元.
(1)在某一时刻内,依次下线10个零件,如果其中出现了不合格品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查若这10个零件的尺寸分别为9.6,10.5,9.8,10.1,10.7,9.4,10.9,9.5,10,10.9,则从这一天抽检的结果看,是否需要对当天的生产过程进行检查?
(2)将样本的估计近似地看作总体的估计通过检验发现,该零件的尺寸![]() 服从正态分布
服从正态分布![]() .其中近似为样本平均数,
.其中近似为样本平均数,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)从下线的零件中随机抽取20件,设其中为合格品的个数为![]() ,求
,求![]() 的数学期望(结果保留整数)
的数学期望(结果保留整数)
(ii)试估计生产10000个零件所获得的利润.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点.
的中点.

(1)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
,![]() 相邻对称轴之间的距离为
相邻对称轴之间的距离为![]() ,且函数
,且函数![]() 在
在![]() 处取得最大值,则下列命题正确的是( )
处取得最大值,则下列命题正确的是( )
①当![]() 时,
时,![]() 的取值范围是
的取值范围是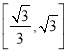 ;
;
②将![]() 的图象向左平移
的图象向左平移![]() 个单位后所对应的函数为偶函数;
个单位后所对应的函数为偶函数;
③函数![]() 的最小正周期为
的最小正周期为![]() ;
;
④函数![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
A.①②B.①③C.①③④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线![]() 焦点,A为抛物线C上的一动点,抛物线C在A处的切线交y轴于点B,以FA、FB为邻边作平行四边形FAMB.
焦点,A为抛物线C上的一动点,抛物线C在A处的切线交y轴于点B,以FA、FB为邻边作平行四边形FAMB.
(1)证明:点M在一条定直线上;
(2)记点M所在定直线为l,与y轴交于点N,MF与抛物线C交于P,Q两点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是抛物线
是抛物线![]() 的焦点,过点
的焦点,过点![]() 且与坐标轴不垂直的直线交抛物线于
且与坐标轴不垂直的直线交抛物线于![]() 、
、![]() 两点,交抛物线的准线于点
两点,交抛物线的准线于点![]() ,其中
,其中![]() ,
,![]() .过点
.过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.

(1)求![]() 的值;
的值;
(2)求四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天文学中为了衡量星星的明暗程度,古希腊天文学家喜帕恰斯(![]() ,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(
,又名依巴谷)在公元前二世纪首先提出了星等这个概念.星等的数值越小,星星就越亮;星等的数值越大,它的光就越暗.到了1850年,由于光度计在天体光度测量中的应用,英国天文学家普森(![]() )又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
)又提出了衡量天体明暗程度的亮度的概念.天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足![]() .其中星等为
.其中星等为![]() 的星的亮度为
的星的亮度为![]() .已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的
.已知“心宿二”的星等是1.00.“天津四” 的星等是1.25.“心宿二”的亮度是“天津四”的![]() 倍,则与
倍,则与![]() 最接近的是(当
最接近的是(当![]() 较小时,
较小时, ![]() )
)
A.1.24B.1.25C.1.26D.1.27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】医院为筛查某种疾病,需要血检,现有![]() 份血液样本,有以下两种检验方式:
份血液样本,有以下两种检验方式:
方式一:逐份检验,需要检验![]() 次;
次;
方式二:混合检验,把每个人的血样分成两份,取![]() 个人的血样各一份混在一起进行检验,如果结果是阴性,那么对这
个人的血样各一份混在一起进行检验,如果结果是阴性,那么对这![]() 个人只作一次检验就够了;如果结果是阳性,那么再对这
个人只作一次检验就够了;如果结果是阳性,那么再对这![]() 个人的另一份血样逐份检验,此时这
个人的另一份血样逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.
次.
(1)假设有6份血液样本,其中只有2份样本为阳性,若采用逐份检验的方式,求恰好经过3次检验就能把阳性样本全部检验岀来的概率;
(2)假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是相互独立的,且每份样本是阳性结果的概率为![]() .现取其中
.现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
①运用概率统计的知识,若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
②若![]() ,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com