
分析 (1)由椭圆的性质可知:e=$\frac{c}{a}$,4a=4$\sqrt{2}$及b2=a2-b2即可求得a、b和c的值,求得椭圆的方程;
(2)由题意设出直线方程x=ny+1,和椭圆方程联立后化为关于y的一元二次方程,由三角形的面积公式写出面积,求得n的值,则直线方程可求.
解答 解:由离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,即a2=2c2,
△ABF1的周长为4$\sqrt{2}$.即4a=4$\sqrt{2}$.
∴a=$\sqrt{2}$,c=1,
由b2=a2-b2=2-1=1,
∴椭圆方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)当斜率不存在时,
当x=1时,y=±$\frac{\sqrt{2}}{2}$,丨AB丨=$\sqrt{2}$,
△ABF1的面积S=$\frac{1}{2}$×2c×丨AB丨=$\sqrt{2}$,不成立,
当斜率存在,过点F2(1,0)直线AB的方程为x=ny+1,
将直线方程代入椭圆方程,得(2+n2)y2+2ny-1=0,
设A(x1,y1),B(x2,y2),
∴y1+y2=$\frac{-2n}{2+{n}^{2}}$,y1•y2=-$\frac{1}{2+{n}^{2}}$,
丨y1-y2丨=$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{2\sqrt{2}\sqrt{1+{n}^{2}}}{2+{n}^{2}}$,
△ABF1的面积S=$\frac{1}{2}$×2c×丨AB丨=$\frac{1}{2}$×2×$\frac{2\sqrt{2}\sqrt{1+{n}^{2}}}{2+{n}^{2}}$=$\frac{2\sqrt{2}\sqrt{1+{n}^{2}}}{2+{n}^{2}}$,
$\frac{2\sqrt{2}\sqrt{1+{n}^{2}}}{2+{n}^{2}}$=$\frac{4}{3}$,整理得:2n4-n2-1=0,解得:n2=1,n=±1,
故直线方程为y-x+1=0或-y-x+1=0.
点评 本题考查椭圆的性质,直线与圆锥曲线的位置关系,考查根与系数的关系、弦长公式、点到直线的距离公式,三角形的面积公式,考查转化思想,推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
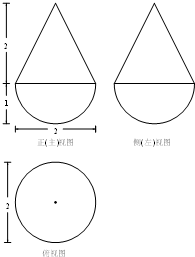
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | 2π | D. | $\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 4 | 6 | 8 | 5 |
| A. | 0.5 | B. | 1 | C. | 1.5 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图所示的三角形数:
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数.他们研究过如图所示的三角形数:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2880 | B. | 7200 | C. | 1440 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com