
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上的最大值是
上的最大值是![]() ,求
,求![]() 的值;
的值;
(3)记![]() ,当
,当![]() 时,若对任意式
时,若对任意式![]() ,总有
,总有![]() 成立,试求
成立,试求![]() 的最大值.
的最大值.
【答案】(1)![]() 在
在![]() 上是增函数;在
上是增函数;在![]() 上是减函数(2)
上是减函数(2)![]() (3)
(3)![]() 的最大值为
的最大值为![]()
【解析】
(1)求得![]() 的定义域和导函数,由此求得
的定义域和导函数,由此求得![]() 的单调区间.
的单调区间.
(2)求得![]() 的导函数
的导函数![]() ,对
,对![]() 分成
分成![]() ,
,![]() ,
,![]() 三种情况,结合
三种情况,结合![]() 在区间
在区间![]() 上的单调性和最大值,求得
上的单调性和最大值,求得![]() 的值.
的值.
(3)首先求得![]() 的的表达式,利用
的的表达式,利用![]() 的导函数
的导函数![]() 判断出当
判断出当![]() 时,
时,![]() 为减函数,由此将不等式
为减函数,由此将不等式![]() 转化为
转化为![]() ,构造函数
,构造函数![]() ,
,![]() 在
在![]() 上为减函数,由
上为减函数,由![]() 的导函数
的导函数![]() 分离常数
分离常数![]() ,得到
,得到![]() ,结合基本不等式,求得
,结合基本不等式,求得![]() 的最大值.
的最大值.
(1)![]() 的定义域是
的定义域是![]() ,
,![]() ,
,
令![]() ,则
,则![]() (舍去),
(舍去),
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上是减函数.
上是减函数.
(2)∵![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
故在![]() 上的最大值为
上的最大值为![]() ,显然不合题意:
,显然不合题意:
②若 即
即![]() 时,
时, ,则
,则![]() 在
在![]() 上是增函数,
上是增函数,
故在![]() 上的最大值为
上的最大值为![]() ,不合超意,舍去;
,不合超意,舍去;
③若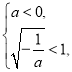 即
即![]() 时,则
时,则![]() 在
在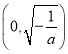 上是增函数,在
上是增函数,在 上是减函数,
上是减函数,
故在在![]() 上的最大值为
上的最大值为![]() ,解得
,解得![]() ,符合,
,符合,
综合①②③得![]() .
.
(3)![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 时,
时,![]() 在
在![]() 上是减函数,
上是减函数,
不妨设![]() ,则
,则![]() ,
,
故![]() 等价于
等价于![]() ,
,
即![]() ,记
,记![]() ,从而
,从而![]() 在
在![]() 上为减函数,
上为减函数,
由![]() ,得
,得![]() ,故
,故![]() 恒成立,
恒成立,
∵![]() ,又
,又![]() 在
在![]() 上单调递减
上单调递减
∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
故![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某公司新发明了甲、乙两种不同型号的手机,公司统计了消费者对这两种型号手机的评分情况,作出如下的雷达图,则下列说法不正确的是( )

A. 甲型号手机在外观方面比较好.B. 甲、乙两型号的系统评分相同.
C. 甲型号手机在性能方面比较好.D. 乙型号手机在拍照方面比较好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,M在线段
,M在线段![]() 上,且
上,且![]() .
.
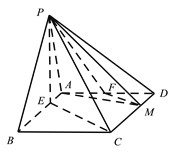
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)在线段AD上确定一点F,使得平面![]() 平面PAB,并求三棱锥
平面PAB,并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年9月15中秋节(农历八月十五)到来之际,某月饼销售企业进行了一项网上调查,得到如下数据:
男 | 女 | 合计 | |
喜欢吃月饼人数(单位:万人) | 50 | 40 | 90 |
不喜欢吃月饼人数(单位:万人) | 30 | 20 | 50 |
合计 | 80 | 60 | 140 |
为了进一步了解中秋节期间月饼的消费量,对参与调查的喜欢吃月饼的网友中秋节期间消费月饼的数量进行了抽样调查,得到如下数据:

已知该月饼厂所在销售范围内有30万人,并且该厂每年的销售份额约占市场总量的35%.
(1)试根据所给数据分析,能否有![]() 以上的把握认为,喜欢吃月饼与性别有关?
以上的把握认为,喜欢吃月饼与性别有关?
参考公式与临界值表: ,
,
其中:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(2)若忽略不喜欢月饼者的消费量,请根据上述数据估计:该月饼厂恰好生产多少吨月饼恰好能满足市场需求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月24日国家统计局在庆祝中华人民共和国成立70周年活动新闻中心举办新闻发布会指出,1952年~2018年,我国GDP查679.1亿元跃升至90.03万亿元,实际增长174倍;人均GDP从119元提高到6.46万元,实际增长70倍.全国各族人民,砥砺奋进,顽强拼搏,实现了经济社会的跨越式发展.如图是全国2010年至2018年GDP总量![]() (万亿元)的折线图.注:年份代码1~9分别对应年份2010~2018.
(万亿元)的折线图.注:年份代码1~9分别对应年份2010~2018.
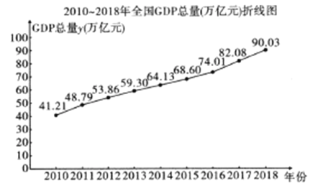
(1)由折线图看出,可用线性回归模型拟合![]() 与年份代码
与年份代码![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),并预测2021年全国GDP的总量.
的回归方程(系数精确到0.01),并预测2021年全国GDP的总量.
附注:参考数据:![]() .
.
参考公式:相关系数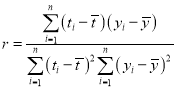 ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为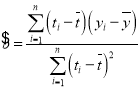 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:其中所有假命题的序号是_______.
①命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ;
;
②将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像;
的图像;
③幂函数![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() ;
;
④函数![]() 有两个零点.
有两个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到定点
到定点![]() 和到直线
和到直线![]() 的距离之比为
的距离之比为![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点作垂直于
,过点作垂直于![]() 轴的直线与曲线
轴的直线与曲线![]() 相交于两点,直线
相交于两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与
两点,与![]() 相交于一点(交点位于线段
相交于一点(交点位于线段![]() 上,且与
上,且与![]() 不重合).
不重合).
(1)求曲线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切时,四边形
相切时,四边形![]() 的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
的面积是否有最大值?若有,求出其最大值及对应的直线的方程;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com